Capítulo 2 Referencial para Inferência
2.1 Modelagem - Primeiras Ideias
Com o objetivo de dar uma primeira ideia sobre o assunto a ser tratado neste livro vamos considerar, numa situação simples, algumas abordagens alternativas para modelagem e análise estatística.
2.1.1 Abordagem 1 - Modelagem Clássica
Seja \(Y\) um vetor \(P \times 1\) de variáveis de pesquisa (ou de interesse), e sejam \(n\) vetores de observações destas variáveis para uma amostra de unidades de interesse denotados por \(y_1, \ldots ,y_n\). Em Inferência Estatística, a abordagem que aqui chamamos de Modelagem clássica considera \(y_1, \ldots ,y_n\) como valores (realizações) de vetores de variáveis aleatórias \(Y_1, \ldots ,Y_n\).
Podemos formular modelos bastante sofisticados para a distribuição conjunta destes vetores aleatórios, mas para simplificar a discussão, vamos inicialmente supor que \(Y_1, \ldots ,Y_n\) são vetores aleatórios independentes e identicamente distribuídos (IID), com a mesma distribuição de \(Y\), caracterizada pela função de densidade ou de frequência \(f(y;\theta)\), onde \(\theta \in \Theta\) é o parâmetro (um vetor de dimensão \(K \times 1\)) indexador da distribuição \(f\), e \(\Theta\) é o espaço paramétrico. A partir das observações \(y_1, \ldots ,y_n\), são feitas inferências a respeito do parâmetro \(\theta\).
Uma representação gráfica esquemática dessa abordagem é apresentada na Figura 2.1, e uma descrição esquemática resumida é apresentada na Tabela 2.1.
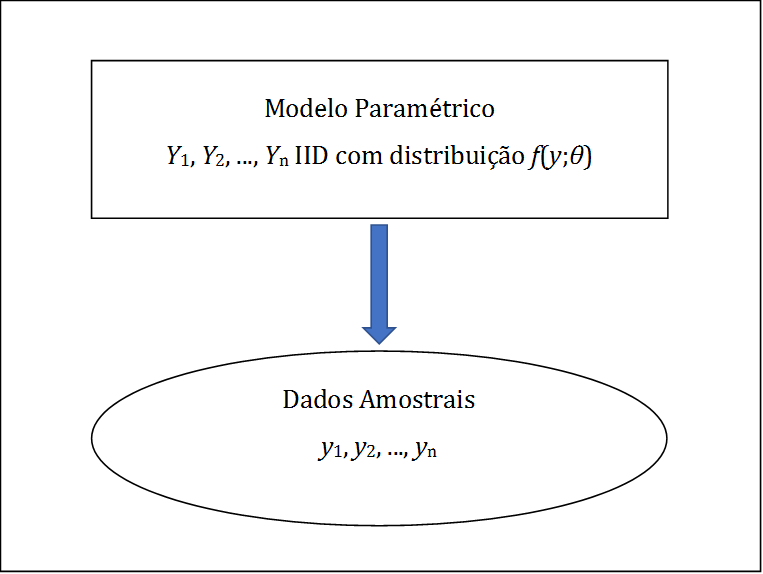
Figura 2.1: Representação esquemática da Modelagem Clássica
| Dados Amostrais | \(Y_1=y_1, \ldots, Y_n=y_n\) |
| Modelo Paramétrico/ Hipóteses | \(Y_1, \ldots ,Y_n\) variáveis aleatórias IID com distribuição \(f(y,\theta)\), onde \(\theta \in \Theta\) |
| Objetivo | Inferir sobre \(\theta\) usando as observações \(y_1, \ldots ,y_n\) |
Do ponto de vista matemático, o parâmetro \(\theta\) serve para indexar os elementos da família de distribuições \(\left\{f\left( y;\theta \right);\theta \in \Theta \right\}\). Na prática, as questões relevantes da pesquisa são traduzidas em termos de perguntas sobre o valor ou região a que pertence o parâmetro \(\theta\), e a inferência sobre \(\theta\) a partir dos dados ajuda a responder tais questões.
Esta abordagem é útil em estudos analíticos tais como, por exemplo, na investigação da natureza da associação entre variáveis (modelos de regressão linear ou logística, modelos log-lineares, etc.). Vários exemplos discutidos ao longo dos Capítulos 6, 7 e 8 ilustram situações deste tipo. No Capítulo 9 o foco vai ser a estimação não paramétrica da forma da função \(f(y;\theta)\).
Inferência sob modelos do tipo descrito nesta seção forma o conteúdo de um curso introdutório de inferência estatística. Mais detalhes podem ser consultados, por exemplo, em (Casella and Berger 2010) e (Magalhães and Lima 2015).
2.1.2 Abordagem 2 - Amostragem Probabilística
A abordagem adotada pelos praticantes de Amostragem Probabilística (amostristas) considera uma população finita \(U=\{1, \ldots ,N\}\), da qual é selecionada uma amostra \(a=\left\{ i_{1}, \ldots ,i_{n}\right\}\), segundo um plano amostral caracterizado por \(p\left( a\right)\), probabilidade de ser selecionada a amostra \(a\), suposta calculável para todas as possíveis amostras. Os valores \(y_{1}, \ldots ,y_{N}\) das variáveis de interesse \(Y\) na população finita são considerados fixos, porém desconhecidos.
A partir dos valores observados na amostra \(a\), denotados por \(y_{i_1}, \ldots, y_{i_n}\), são feitas inferências a respeito de funções dos valores populacionais, digamos \(g\left( y_{1}, \ldots , y_{N}\right)\). Os valores de tais funções são quantidades descritivas populacionais (QDPs), também denominadas parâmetros da população finita pelos amostristas. Em geral, o objetivo desta abordagem é fazer estudos descritivos utilizando funções \(g\) particulares, tais como totais \(g\left( y_{1}, \ldots , y_{N}\right) = \sum_{i=1}^{N} y_{i}\) , médias \(g\left( y_{1}, \ldots , y_{N}\right) = N^{-1}\sum_{i=1}^{N} y_{i}\), proporções, razões, etc. Uma descrição esquemática resumida dessa abordagem é apresentada na Tabela 2.2, e uma representação gráfica resumida na Figura 2.2.
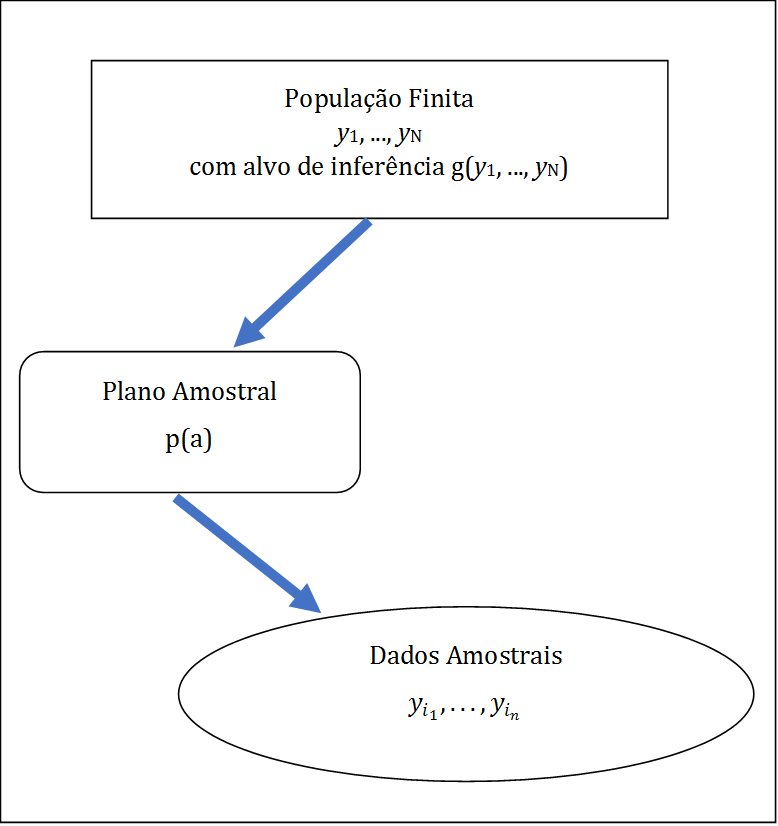
Figura 2.2: Amostragem Probabilística
| Dados Amostrais | \(Y_1=y_{i_1}, \ldots, Y_n=y_{i_n}\) |
| Hipóteses/Modelo Hipóteses | extraídos de \(y_1, \ldots , y_N\) segundo \(p(a)\) |
| Objetivo | Inferir sobre funções \(g(y_1, \ldots , y_N)\) usando \(y_{i_1}, \ldots, y_{i_n}\) |
Esta abordagem é largamente empregada na produção de estatísticas públicas e oficiais, por agências e instituições de muitos países. Uma das alegadas vantagens dessa abordagem é o fato de que as distribuições de referência usadas para inferência são controladas pelos amostristas que planejam as pesquisas por amostragem, e portanto, a inferência pode ser considerada não paramétrica e não dependente de modelos que precisariam ser especificados pelo analista.
2.1.3 Discussão das Abordagens 1 e 2
A primeira abordagem ( Modelagem Clássica ), nos termos descritos, foi inicialmente proposta para dados de medidas na Física e Astronomia, onde em geral o pesquisador tem relativo controle sobre os experimentos, e onde faz sentido falar em replicação ou repetição do experimento. Neste contexto, a ideia de aleatoriedade é geralmente introduzida para modelar os erros (não controláveis) do processo de medição, e as distribuições de estatísticas de interesse são derivadas a partir da distribuição do modelo especificado.
A segunda abordagem ( Amostragem Probabilística ) é utilizada principalmente no contexto de estudos socioeconômicos observacionais, para levantamento de dados por agências governamentais produtoras de informações estatísticas. Nesta abordagem, a aleatoriedade é introduzida pelo pesquisador no processo para obtenção dos dados, através do planejamento amostral \(p(a)\) utilizado (Neyman 1934) e as distribuições das estatísticas de interesse são derivadas a partir dessa distribuição de aleatorização.
Os planos amostrais podem ser complexos, gerando observações afetadas pelas características i) a iv) mencionadas no Capítulo 1. Os dados obtidos são utilizados principalmente para descrição da população finita, mediante o cálculo de estimativas de parâmetros descritivos usuais tais como totais, médias, proporções, razões, etc. Sob a abordagem de Amostragem Probabilística, os pontos i) a iv) do Capítulo 1 são devidamente considerados tanto na estimação dos parâmetros descritivos como também na estimação de variâncias dos estimadores, permitindo a inferência pontual e por intervalos de confiança baseada na distribuição assintótica normal dos estimadores habitualmente considerados.
A abordagem de Amostragem Probabilística é essencialmente não-paramétrica, pois não supõe uma distribuição paramétrica particular para as observações da amostra. Por outro lado, essa abordagem tem a desvantagem de fazer inferências restritas à particular população finita considerada.
Apesar da abordagem de Amostragem Probabilística ter sido inicialmente concebida e aplicada para problemas de inferência descritiva sobre populações finitas, é cada vez mais comum, porém, a utilização dos dados obtidos através de pesquisas amostrais complexas para fins analíticos, com a aplicação de métodos de análise desenvolvidos e apropriados para a abordagem de Modelagem Clássica. Nesse contexto, é relevante considerar algumas questões de interesse.
É adequado aplicar métodos de análise da Modelagem Clássica, concebidos para observações IID, aos dados obtidos através de pesquisas amostrais complexas?
Em caso negativo, seria possível corrigir estes métodos, tornando-os aplicáveis para tratar dados amostrais complexos?
Ou seria mais adequado fazer uso analítico dos dados dentro da abordagem de Amostragem Probabilística? E neste caso, como fazer isto, visto que nesta abordagem não é especificado um modelo para a distribuição das variáveis de pesquisa na população?
Além destas questões, também é de interesse a questão da robustez da inferência, traduzida nas seguintes perguntas.
O que acontece quando o modelo adotado na Modelagem Clássica não é verdadeiro?
- Neste caso, qual a interpretação dos parâmetros na Modelagem Clássica?
Ainda neste caso, as quantidades descritivas populacionais da Amostragem Probabilística poderiam ter alguma utilidade ou interpretação?
O objeto deste livro é exatamente discutir respostas para as questões aqui enumeradas. Para isso, vamos considerar uma abordagem que propõe um modelo parametrizado como na Modelagem Clássica, mas formulado para descrever os dados da população, e não os da amostra. Além disso, essa abordagem incorpora na análise os pontos i) a iii) do Capítulo 1 mediante aproveitamento da estrutura do planejamento amostral, como feito habitualmente na Amostragem Probabilística. Essa abordagem, denominada de Modelagem de Superpopulação, foi primeiro proposta em (???) e (Royall 1970), e é bem descrita, por exemplo, em (Binder 1983) e (Valliant and Royall 2000).
2.1.4 Abordagem 3 - Modelagem de Superpopulação
Nesta abordagem, os valores \(y_{1}, \ldots ,y_{N}\) das variáveis de interesse \(Y\) na população finita são considerados observações ou realizações dos vetores aleatórios \(Y_{1}, \ldots , Y_{N}\), supostos IID com distribuição \(f(y;\theta)\), onde \(\theta \in \Theta\). Este modelo é denominado Modelo de Superpopulação. Note que, em contraste com o que se faz na Modelagem Clássica, o modelo probabilístico é aqui especificado para descrever o mecanismo aleatório que gera a população, não a amostra. Na maioria das aplicações práticas, a população de interesse, embora considerada finIta, jamais será observada por inteiro. Não obstante, ao formular o modelo para descrever propriedades da população, nossas perguntas e respostas descritas em termos de valores ou regiões para o parâmetro \(\theta\) passam a se referir à população de interesse ou a populações similares, quer existam ao mesmo tempo, quer se refiram a estados futuros (ou passados) da mesma população. Vale realçar também que pesquisas por amostragem “consistem em selecionar parte de uma população para observar, de modo que seja possível estimar alguma coisa sobre toda a população”, conforme (Thompson 1992).
Utilizando um plano amostral definido por \(p(a)\), obtemos os valores das variáveis de pesquisa na amostra \(y_{i_1}, \ldots , y_{i_n}\). A partir de \(y_{i_1}, \ldots , y_{i_n}\), em geral não considerados como observações de vetores aleatórios IID, queremos fazer inferência sobre o parâmetro \(\theta\), considerando os pontos i) a iii) do Capítulo 1. Veja uma representação gráfica resumida desta abordagem na Figura 2.3.
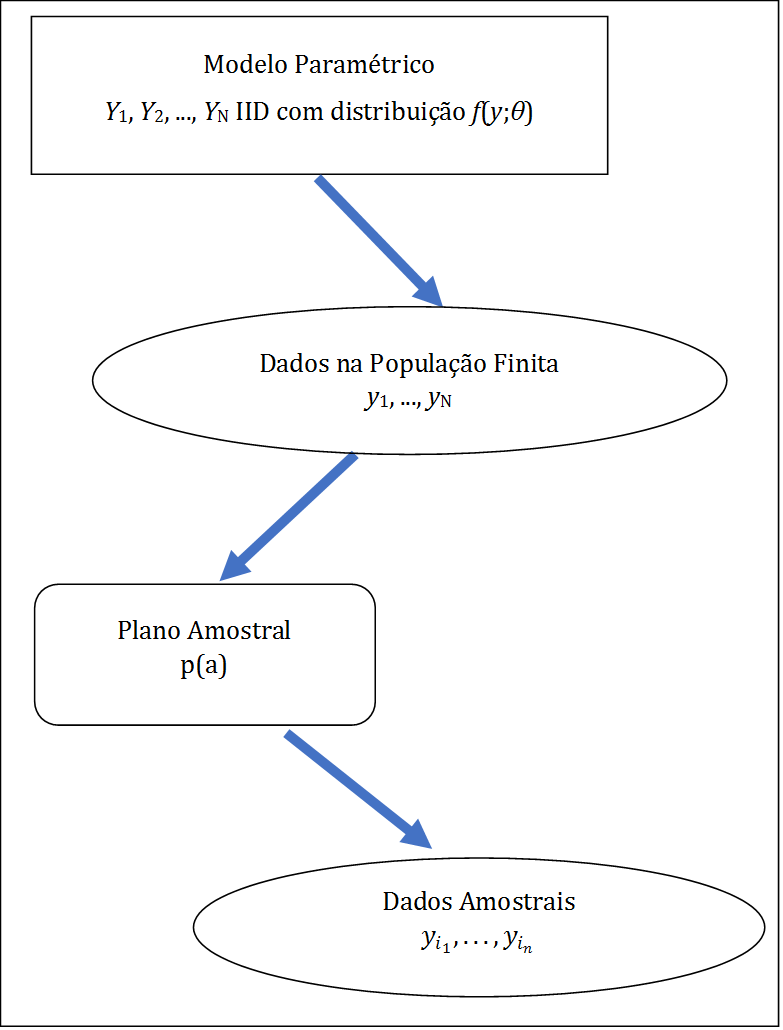
Figura 2.3: Modelagem de Superpopulação
Adotando o Modelo de Superpopulação e considerando métodos usuais disponíveis na Modelagem Clássica, podemos utilizar funções de \(y_{1}, \ldots ,y_{N}\) , digamos \(g( y_{1}, \ldots , y_{N})\), para fazer inferência sobre \(\theta\). Desta forma, definimos estatísticas \(\left( y_{1},\ldots ,y_{N}\right)\) (no sentido da Modelagem Clássica) que são quantidades descritivas populacionais (parâmetros populacionais no contexto da Amostragem Probabilística), que passam a ser os novos parâmetros-alvo. O passo seguinte é utilizar métodos disponíveis na Amostragem Probabilística para fazer inferência sobre \(g\left( y_{1}, \ldots , y_{N}\right)\) baseada em \(y_{i_1},\ldots ,y_{i_n}\). Note que não é possível basear a inferência nos valores populacionais \(y_{1}, \ldots , y_{N}\), já que estes não são conhecidos ou observados. Este último passo adiciona a informação sobre o plano amostral utilizado, contida em \(p(a)\), à informação estrutural contida no modelo \(\left\{ f\left( y; \theta \right) ;\theta \in \Theta\right\}\). Uma representação esquemática dessa abordagem é apresentada na Tabela 2.3.
| Dados Amostrais | \(Y_1=y_{i_1},\ldots,Y_n=y_{i_n}\) |
| População e esquema de seleção | Extraídos de \(y_1,\dots,y_N\) segundo \(p(a)\) |
| Modelo para população | \(Y_1, \dots, Y_N\) variáveis aleatórias IID com distribuição \(f(y,\theta)\), onde \(\theta \in \Theta\) |
| Parâmetro-alvo | associar \(\theta \longleftrightarrow g\left(Y_{1}, \ldots , Y_{N}\right)\) |
| Objetivo | Inferir sobre \(g\left( Y_{1}, \ldots , Y_{N}\right)\) partir de \(y_{i_1},\ldots,y_{i_n}\) usando \(p\left( a\right)\) |
A descrição da abordagem adotada neste livro foi apresentada de maneira propositalmente simplificada e vaga nesta seção, mas será aprofundada ao longo do texto. Admitiremos que o leitor esteja familiarizado com a Modelagem Clássica e com as noções básicas da Amostragem Probabilística. A título de recordação, serão apresentados no Capítulo 2.4 alguns resultados básicos da Amostragem Probabilística. A ênfase do texto, porém, será na apresentação da Modelagem de Superpopulação, sendo para isto apresentados os elementos indispensáveis das abordagens de Modelagem Clássica e da Amostragem Probabilística.
Ao construir e ajustar modelos a partir de dados de pesquisas amostrais complexas, tais como as executadas pelo IBGE e outras instituições similares, o usuário precisa incorporar as informações sobre pesos e sobre a estrutura dos planos amostrais utilizados. Em geral, ao publicar os resultados das pesquisas, os pesos são considerados, sendo possível produzir estimativas pontuais corretas utilizando os pacotes tradicionais. Por outro lado, para construir intervalos de confiança e testar hipóteses sobre parâmetros de modelos, seria preciso o conhecimento das estimativas de variâncias e covariâncias das estimativas, obtidas levando em conta a estrutura do plano amostral utilizado. Mesmo conhecendo o plano amostral, geralmente não é simples incorporar pesos e plano amostral na análise sem o uso de pacotes especializados, ou de rotinas específicas já agora disponíveis em alguns dos pacotes mais comumente utilizados (por exemplo, SAS, Stata, SPSS, ou R entre outros). Tais pacotes especializados ou rotinas específicas utilizam, em geral, métodos aproximados para estimar matrizes de covariância. Entre esses métodos, destacam-se o de Máxima Pseudo-Verossimilhança, a Linearização, o método do Conglomerado Primário, e métodos de reamostragem, que serão descritos mais adiante.
Em outras palavras, o uso dos pacotes usuais para analisar dados produzidos por pesquisas com planos amostrais complexos, tal como o uso de muitos remédios, pode ter contra-indicações. Cabe ao usuário ler a bula e identificar situações em que o uso de tais pacotes pode ser inadequado, e buscar opções de rotinas específicas ou de pacotes especializados capazes de incorporar adequadamente a estrutura do plano amostral nas análises.
Ao longo deste livro faremos uso intensivo do pacote survey disponível no R, mas o leitor encontrará funcionalidade semelhante em vários outros pacotes. Nossa escolha se deveu a dois fatores principais: primeiro ao fato do pacote R ser aberto, livre e gratuito, dispensando o usuário de custos de licenciamento, bem como possibilitando aos interessados o acesso ao código fonte e à capacidade de modificar as rotinas de análise, caso necessário. O segundo fator é de natureza mais técnica, porém transitória. No presente momento, o pacote survey é a coleção de rotinas mais completa e genérica existente para análise de dados amostrais complexos, dispondo de funções capazes de ajustar os modelos usuais, mas também de ajustar modelos não convencionais, mediante a maximização numérica de verossimilhanças especificadas pelo usuário. Sabemos, entretanto, que muitos usuários habituados à facilidade de uso de pacotes com interfaces gráficas do tipo aponte e clique terão dificuldade adicional de adaptar-se à linguagem de comandos utilizada pelo pacote R, mas acreditamos que os benefícios do aprendizado desta nova ferramenta compensarão largamente os custos adicionais do aprendizado.
O emprego de ferramentas de análise como o pacote survey permitirá aos usuários focar sua atenção mais na seleção, análise e interpretação dos modelos ajustados do que nas dificuldades técnicas envolvidas nos cálculos correspondentes. É com este espírito que escrevemos este texto, que busca apresentar os métodos, ilustrando seu uso com exemplos reais, e orientando sobre o uso adequado das ferramentas de modelagem e análise disponíveis no sistema R.
2.2 Fontes de Variação
Esta seção estabelece o referencial para inferência em pesquisas amostrais que será usado no restante deste texto. (Cassel, Särndal, and Wretman 1977) sugerem que um referencial para inferência poderia considerar três fontes de aleatoriedade (incerteza, variação), incluindo:
Modelo de Superpopulação, que descreve o processo subjacente que, por hipótese, gera as medidas verdadeiras para todas as unidades da população considerada;
Processo de Medição, que diz respeito aos instrumentos e métodos usados para obter as medidas de qualquer unidade da população;
Planejamento Amostral, que estabelece o mecanismo pelo qual unidades da população são selecionadas para participar da amostra da pesquisa ou estudo.
Uma quarta fonte de incerteza que precisa ser acrescentada às anteriores é o
- Mecanismo de resposta, ou seja, o mecanismo que controla se valores de medições de unidades selecionadas para a amostra são obtidos / observados ou não.
Para concentrar o foco nas questões de maior interesse deste texto, as fontes (2) e (4) não serão consideradas no referencial adotado para a maior parte dos capítulos. Para o tratamento das dificuldades causadas por não resposta, a fonte (4) será considerada no capítulo onze. Assim sendo, exceto onde explicitamente indicado, de agora em diante admitiremos que não há erros de medição, implicando que os valores observados de quaisquer variáveis de interesse serão considerados valores corretos ou verdadeiros. Admitiremos ainda que há resposta completa, implicando que os valores de quaisquer variáveis de interesse estão disponíveis para todos os elementos da amostra selecionada depois que a pesquisa foi realizada. Hipóteses semelhantes são adotadas, por exemplo, em (Binder 1983) e (Montanari 1987).
Portanto, o referencial aqui adotado considera apenas duas fontes alternativas de variação: o Modelo de Superpopulação (1) e o Plano Amostral (3). Estas fontes alternativas de variação, descritas nesta seção apenas de forma esquemática, são discutidas com maiores detalhes a seguir.
A fonte de variação (1) será considerada porque usos analíticos das pesquisas são amplamente discutidos neste texto, os quais só têm sentido quando é especificado um modelo estocástico para o processo subjacente que gera as medidas na população. A fonte de variação (3) será considerada porque a atenção será focalizada na análise de dados obtidos através de pesquisas amostrais complexas. Aqui a discussão se restringirá a planos amostrais aleatorizados ou de Amostragem Probabilística, não sendo considerados métodos intencionais ou outros métodos não-aleatórios algumas vezes usados para seleção de amostras.
2.3 Modelos de Superpopulação
Seja \(\{1, ..., N\}\) um conjunto de rótulos que identificam univocamente os \(N\) elementos distintos de uma população-alvo finita \(U\). Sem perda de generalidade tomaremos \(U=\{1,...,N\}\). Uma pesquisa cobrindo \(n\) elementos distintos numa amostra \(a\), \(a=\{i_{1},...,i_{n}\}\subset U\), é realizada para medir os valores de \(P\) variáveis de interesse da pesquisa, doravante denominadas simplesmente variáveis da pesquisa.
Denotaremos por \(\mathbf{y}_i=(y_{i1},...,y_{iP})^{\prime }\) o vetor \(P\times 1\) de valores das variáveis da pesquisa e por \(\mathbf{x}_{i}=(x_{i1},...,x_{iQ})^{\prime }\) o vetor \(Q\times 1\) de variáveis auxiliares da i-ésima unidade da população, respectivamente, para \(i=1,...,N\). Aqui as variáveis auxiliares são consideradas como variáveis contendo a informação requerida para o planejamento amostral e a estimação a partir da amostra, como se discutirá com mais detalhes adiante. Denote por \(\mathbf{y}_{U}\) a matriz \(N \times P\) formada empilhando os vetores transpostos das observações das variáveis de pesquisa correspondentes a todas as unidades da população, e por \(\mathbf{Y}_{U}\) a correspondente matriz de vetores aleatórios geradores das observações na população.
Quando se supõe que \(\mathbf{y}_1 ,\ldots, \mathbf{y}_N\) são a realização conjunta de vetores aleatórios \(\mathbf{Y}_1 ,\ldots, \mathbf{Y}_N\), a distribuição conjunta de probabilidade de \(\mathbf{Y}_1 ,\ldots, \mathbf{Y}_N\) é um Modelo de Superpopulação (marginal), que doravante denotaremos simplesmente por \(f(\mathbf{y}_U;\theta)\), ou de forma abreviada, por \(M\). Esperanças e variâncias definidas com respeito à distribuição do modelo \(M\) serão denotadas \(E_M\) e \(V_M\) respectivamente.
Analogamente, \(\mathbf{x}_1 ,\ldots, \mathbf{x}_N\) pode ser considerada uma realização conjunta de vetores aleatórios \(\mathbf{X}_1 ,\ldots, \mathbf{X}_N\). As matrizes \(N \times Q\) formadas empilhando os vetores transpostos das observações das variáveis auxiliares correspondentes a todas as unidades da população, \(\mathbf{x}_{U}\), e a correspondente matriz \(\mathbf{X}_{U}\) de vetores aleatórios geradores das variáveis auxiliares na população são definidas de forma análoga às matrizes \(\mathbf{y}_{U}\) e \(\mathbf{Y}_{U}\).
O referencial aqui adotado permite a especificação da distribuição conjunta combinada das variáveis da pesquisa e das variáveis auxiliares. Representamos por \(f( \mathbf{y}_U , \mathbf{x}_U ; \mathbf{\eta} )\) a função de densidade de probabilidade conjunta de \(( \mathbf{Y}_U , \mathbf{X}_U )\), onde \(\mathbf{\eta}\) é um vetor de parâmetros.
Um tipo importante de modelo de superpopulação é obtido quando os vetores aleatórios correspondentes às observações de unidades diferentes da população são supostos independentes e identicamente distribuídos (IID). Neste caso, o modelo de superpopulação pode ser escrito como:
\[\begin{eqnarray} f \left( \mathbf{y}_U , \mathbf{x}_U ; \mathbf{\eta} \right) &=&\prod_{i\in U} f\left(\mathbf{y}_i , \mathbf{x}_i ; \mathbf{\eta} \right) \tag{2.1} \\ &=&\prod_{i\in U} f\left( \mathbf{y}_i \mathbf{|x}_i ; \mathbf{\lambda} \right) f\left( \mathbf{x}_i ; \mathbf{\phi} \right) \tag{2.2} \end{eqnarray}\]onde \(\mathbf{\lambda}\) e \(\mathbf{\phi}\) são vetores de parâmetros.
Sob (2.2), o modelo marginal correspondente das variáveis da pesquisa seria obtido integrando nas variáveis auxiliares:
\[\begin{equation} f(\mathbf{y}_U ; \mathbf{\theta}) = f(\mathbf{y}_1 ,\ldots ,\mathbf{y}_N ; \mathbf{\theta}) = \prod_{i\in U} \int f\left( \mathbf{y}_i \mathbf{|x}_i ; \mathbf{\lambda} \right) f\left( \mathbf{x}_i ; \mathbf{\phi} \right) \mathbf{dx}_i = \prod_{i\in U} f\left( \mathbf{y}_i ; \mathbf{\theta} \right) \tag{2.3} \end{equation}\]onde \(f\left( \mathbf{y}_i ; \mathbf{\theta} \right) = \int f\left( \mathbf{y}_i | \mathbf{x}_i ; \mathbf{\lambda} \right) f\left( \mathbf{x}_i ; \mathbf{\phi} \right) \mathbf{dx}_i\) e \(\mathbf{\theta =} h\left( \mathbf{\lambda} , \mathbf{\phi} \right)\).
Outro tipo especial de modelo de superpopulação é o modelo de população fixa, que supõe que os valores numa população finita são fixos mas desconhecidos. Este modelo pode ser descrito por:
\[\begin{equation} P\left[ \left( \mathbf{Y}_U , \mathbf{X}_U \right) = \left( \mathbf{y}_U , \mathbf{x}_U \right) \right] = 1 \tag{2.4} \end{equation}\]ou seja, uma distribuição degenerada é especificada para \(\left(\mathbf{Y}_U , \mathbf{X}_U \right)\).
Este modelo foi considerado em (Cassel, Särndal, and Wretman 1977), que o chamaram de abordagem de população fixa, e afirmaram ser esta a abordagem subjacente ao desenvolvimento da teoria da Amostragem Probabilística encontrada nos livros clássicos tais como (Cochran 1977) e outros. Aqui esta abordagem é chamada de abordagem baseada no planejamento amostral ou abordagem de aleatorização, pois neste caso a única fonte de variação (aleatoriedade) é proveniente do planejamento amostral. Em geral, a distribuição conjunta de \(\left( \mathbf{Y}_U , \mathbf{X}_U \right)\) não precisa ser degenerada como em (2.4), embora o referencial aqui adotado seja suficientemente geral para permitir considerar esta possibilidade.
Se todas as unidades da população fossem pesquisadas (ou seja, se fosse executado um censo), os dados observados seriam \((\mathbf{y}_1 , \mathbf{x}_1) ,\ldots, (\mathbf{y}_N , \mathbf{x}_N)\). Sob a hipótese de resposta completa, a única fonte de incerteza seria devida ao fato de que \((\mathbf{y}_1 , \mathbf{x}_1) ,\ldots, (\mathbf{y}_N , \mathbf{x}_N)\) é uma realização de \(\left( \mathbf{Y}_1 , \mathbf{X}_1 \right) ,\ldots, \left( \mathbf{Y}_N , \mathbf{X}_N \right)\). Os dados observados poderiam então ser usados para fazer inferências sobre \(\mathbf{\eta}, \mathbf{\phi},\mathbf{\lambda}\) ou \(\mathbf{\theta}\) usando procedimentos padrões.
Inferência sobre quaisquer dos parâmetros \(\mathbf{\eta},\mathbf{\phi},\mathbf{\lambda}\) ou \(\mathbf{\theta}\) do modelo de superpopulação é chamada inferência analítica. Este tipo de inferência só faz sentido quando o modelo de superpopulação não é degenerado como em (2.4). Usualmente seu objetivo é explicar a relação entre variáveis não apenas para a população finita sob análise, mas também para outras populações que poderiam ter sido geradas pelo modelo de superpopulação adotado. Vários exemplos de inferência analítica serão discutidos ao longo deste livro.
Se o objetivo da inferência é estimar quantidades que fazem sentido somente para a população finita sob análise, tais como funções \(g\left( \mathbf{y}_1 ,\ldots, \mathbf{y}_N \right)\) dos valores das variáveis da pesquisa, o modelo de superpopulação não é estritamente necessário, embora possa ser útil. Inferência para tais quantidades, chamadas parâmetros da população finita ou quantidades descritivas populacionais (QDPs), é chamada inferência descritiva.
Vale notar que a especificação do modelo de superpopulação aqui proposta serve tanto para o caso da abordagem clássica para inferência, como também para o caso da abordagem Bayesiana. Neste caso, a especificação do modelo precisaria ser completada mediante a especificação de distribuições a priori para os parâmetros do modelo.
2.4 Planejamento Amostral
Embora censos sejam algumas vezes realizados para coletar dados sobre certas populações, a vasta maioria das pesquisas realizadas é de pesquisas amostrais, nas quais apenas uma amostra de elementos da população (usualmente uma pequena parte) é investigada. Neste caso, os dados disponíveis incluem:
O conjunto de rótulos \(a=\left\{ i_1 , \ldots, i_n \right\}\) dos distintos elementos na amostra, onde \(n\) \(\left( 1 \leq n \leq N \right)\) é o número de elementos na amostra \(a\), também chamado de tamanho da amostra;
Os valores na amostra das variáveis da pesquisa \(\mathbf{y}_{i_1} ,\ldots, \mathbf{y}_{i_n}\);
Os valores das variáveis auxiliares na população \(\mathbf{x}_1 ,\ldots, \mathbf{x}_N\), quando a informação auxiliar é dita completa; alternativamente, os valores das variáveis auxiliares na amostra \(\mathbf{x}_{i_1} ,\ldots, \mathbf{x}_{i_n}\), mais os totais ou médias destas variáveis na população, quando a informação auxiliar é dita parcial.
O mecanismo usado para selecionar a amostra \(a\) da população finita \(U\) é chamado plano amostral. Uma forma de caracterizá-lo é através da função \(p\left( .\right)\), onde \(p(a)\) dá a probabilidade de selecionar a amostra \(a\) no conjunto \(A\) de todas as amostras possíveis. Só mecanismos amostrais envolvendo alguma forma de seleção probabilística bem definida serão aqui considerados. Portanto, supõe-se que \(0 \leq p(a) \leq 1 \; \forall a \in A\) e \(\sum_{a \in A} p(a)=1\).
Esta caracterização do plano amostral \(p(a)\) é bem geral, permitindo que o mecanismo de seleção amostral dependa dos valores das variáveis auxiliares \(\mathbf{x}_1 ,\ldots, \mathbf{x}_N\) bem como dos valores das variáveis da pesquisa na população \(\mathbf{y}_1 ,\ldots, \mathbf{y}_N\) (amostragem informativa, veja Seção 2.5. Uma notação mais explícita para indicar esta possibilidade envolveria escrever \(p(a)\) como \(p\left[ a | (\mathbf{y}_U , \mathbf{x}_U ) \right]\). Tal notação será evitada por razões de simplicidade.
Denotamos por \(I(B)\) a função indicadora que assume o valor 1 quando o evento \(B\) ocorre e 0 caso contrário. Seja \(\mathbf{\Delta}_a = \left[ I(1 \in a) ,\ldots, I(N \in a)\right]^{\prime}\) um vetor aleatório de indicadores dos elementos incluídos na amostra \(a\). Então o plano amostral pode ser alternativamente caracterizado pela distribuição de probabilidade de \(\mathbf{\Delta }_a\) denotada por \(f\left[ \mathbf{\delta }_a | \left(\mathbf{y}_U , \mathbf{x}_U \right) \right]\), onde \(\mathbf{\delta }_a\) é qualquer realização particular de \(\mathbf{\Delta }_a\) tal que \({\mathbf{\delta}_a}^{\prime} \mathbf{1}_N = n\), e \(\mathbf{1}_N\) é o vetor unitário de dimensão \(N\).
Notação adicional necessária nas seções posteriores será agora introduzida. Denotamos por \(\pi_i\) a probabilidade de inclusão da unidade \(i\) na amostra \(a\), isto é,
\[\begin{equation} \pi_i = Pr\left( i \in a \right) = \sum_{a \ni i} p(a) \tag{2.5} \end{equation}\]e denotamos por \(\pi_{ij}\) a probabilidade de inclusão conjunta na amostra das unidades \(i\) e \(j\), dada por
\[\begin{equation} \pi_{ij} = Pr \left( i \in a , j \in a \right) = \sum_{a \ni i,j} p(a) \tag{2.6} \end{equation}\]para todo \(i \neq j \in U\), e seja \(\pi_{ii} = \pi_{i}\) \(\forall i \in U.\)
Uma hipótese básica assumida com relação aos planos amostrais aqui considerados é que \(\pi_i > 0\) e \(\pi_{ij} > 0\) \(\forall i,j \in U.\) A hipótese de \(\pi_{ij}\) ser positiva é adotada para simplificar a apresentação de expressões para estimadores de variância dos estimadores dos parâmetros de interesse. Contudo, esta não é uma hipótese crucial, pois há planos amostrais que não a satisfazem e para os quais estão disponíveis aproximações e estimadores satisfatórios das variâncias dos estimadores de totais e de médias.
2.5 Planos Amostrais Informativos e Ignoráveis
Ao fazer inferência usando dados de pesquisas amostrais precisamos distinguir duas situações que requerem tratamento diferenciado. Uma dessas situações ocorre quando o plano amostral empregado para coletar os dados é informativo, isto é, quando o mecanismo de seleção das unidades amostrais pode depender dos valores das variáveis de pesquisa. Um exemplo típico desta situação é o dos estudos de caso-controle, em que a amostra é selecionada de tal forma que há casos (unidades com determinada condição) e controles (unidades sem essa condição), sendo de interesse a modelagem do indicador de presença ou ausência da condição em função de variáveis preditoras, e sendo esse indicador uma das variáveis de pesquisa, que é considerada no mecanismo de seleção da amostra. Os métodos que discutiremos ao longo deste livro não são adequados, em geral, para esse tipo de situação, e portanto uma hipótese fundamental adotada ao longo deste texto é que os planos amostrais considerados são não-informativos, isto é, não podem depender diretamente dos valores das variáveis da pesquisa. Logo eles satisfazem:
\[\begin{equation} f\left[ \mathbf{\delta }_a | \left( \mathbf{y}_U , \mathbf{x}_U \right) \right] = f\left( \mathbf{\delta }_a | \mathbf{x}_U \right) . \tag{2.7} \end{equation}\]Entre os planos amostrais não-informativos, precisamos ainda distinguir duas outras situações de interesse. Quando o plano amostral é Amostragem Aleatória Simples Com Reposição (AASC), o modelo adotado para a amostra é o mesmo que o modelo adotado para a população antes da amostragem. Quando isto ocorre, o plano amostral é dito ignorável, porque a inferência baseada na amostra utilizando a abordagem DE Modelagem Clássica descrita em 2.1 pode prosseguir sem problemas. Entretanto, esquemas amostrais desse tipo são raramente empregados na prática, por razões de eficiência e custo. Em vez disso, são geralmente empregados planos amostrais envolvendo estratificação, conglomeração e probabilidades desiguais de seleção ( amostragem complexa ).
Com amostragem complexa, porém, os modelos para a população e a amostra podem ser muito diferentes (plano amostral não-ignorável), mesmo que o mecanismo de seleção não dependa das variáveis de pesquisa, mas somente das variáveis auxiliares. Neste caso, ignorar o plano amostral pode viciar a inferência. Veja o Exemplo 2.1 adiante.
A definição precisa de ignorabilidade e as condições sob as quais um plano amostral é ignorável para inferência são bastante discutidas na literatura - veja por exemplo (Sugden and Smith 1984) ou os Capítulos 1 e 2 de (Chambers and Skinner 2003). Porém testar a ignorabilidade do plano amostral é muitas vezes complicado. Em caso de dificuldade, o uso dos pesos amostrais tem papel fundamental, como se verá mais adiante.
Uma forma simples de lidar com os efeitos do plano amostral na estimação pontual de quantidades descritivas populacionais de interesse é incorporar pesos adequados na análise, como se verá no Capítulo 3. Essa forma porém, não resolve por si só o problema de estimação da precisão das estimativas pontuais, nem mesmo o caso da estimação pontual de parâmetros em modelos de superpopulação, o que vai requerer métodos específicos discutidos no Capítulo 5.
Como incluir os pesos para proteger contra planos amostrais não-ignoráveis e a possibilidade de má especificação do modelo? Uma ideia é modificar os estimadores dos parâmetros de modo que sejam consistentes (em termos da distribuição de aleatorização) para quantidades descritivas da população finita da qual a amostra foi extraída, que por sua vez seriam boas aproximações para os parâmetros dos modelos de interesse. Afirmações probabilísticas são então feitas com respeito à distribuição de aleatorização das estatísticas amostrais \(p\) ou com respeito à distribuição mista ou combinada \(Mp\).
A seguir apresentamos um exemplo com a finalidade de ilustrar uma situação de plano amostral não-ignorável.
Considere \(N\) observações de uma população finita \(U\) onde são consideradas de interesse duas variáveis binárias \((x_i ; y_i )\). Suponha que na população os vetores aleatórios \((X_i ; Y_i )\) são independentes e identicamente distribuídos com distribuição de probabilidades conjunta dada por:
| \(y\) | |||
|---|---|---|---|
| \(x\) | 0 | 1 | Total |
| 0 | \(\eta_{00}\) | \(\eta_{01}\) | \(\eta_{0+}\) |
| 1 | \(\eta_{10}\) | \(\eta_{11}\) | \(\eta_{1+}\) |
| Total | \(\eta_{+0}\) | \(\eta_{+1}\) | 1 |
que também pode ser representada por:
\[\begin{eqnarray} f_U (x ; y) &=& Pr( X = x ; Y = y )\\ & =& \eta_{00}^{(1-x)(1-y)} \times \eta_{01}^{(1-x)y} \times \eta_{10}^{x(1-y)} \times (1 - \eta_{00} - \eta_{01} - \eta_{10})^{xy} \nonumber \end{eqnarray}\]onde a designação \(f_U\) é utilizada para denotar a distribuição na população.
Note agora que a distribuição marginal da variável \(Y\) na população é Bernoulli com parâmetro \(1 - \eta_{00} - \eta_{10}\), ou alternativamente:
\[\begin{equation} f_U (y) = Pr( Y = y ) = (\eta_{00} + \eta_{10})^{(1-y)} \times (1 - \eta_{00} - \eta_{10})^y \end{equation}\]De forma análoga, a distribuição marginal da variável \(X\) na população também é Bernoulli, mas com parâmetro \(1 - \eta_{00} - \eta_{01}\), ou alternativamente:
\[\begin{equation} f_U (x) = Pr( X = x ) = (\eta_{00} + \eta_{01})^{(1-x)} \times (1 - \eta_{00} - \eta_{01})^x \end{equation}\]Seja \(N_{xy}\) o número de unidades na população com a combinação de valores observados \((x;y)\), onde \(x\) e \(y\) tomam valores em \(\Omega = \{ 0 ; 1 \}\). É fácil notar então que o vetor de contagens populacionais \(\mathbf{N} = ( N_{00}, N_{01}, N_{10}, N_{11} )^{\prime}\) tem distribuição Multinomial com parâmetros \(N\) e \(\mathbf{\eta} = (\eta_{00} , \eta_{01} , \eta_{10} , 1 - \eta_{00} - \eta_{01} - \eta_{10} )^{\prime}\).
Após observada uma realização do modelo que dê origem a uma população, como seria o caso da realização de um censo na população, a proporção de valores de \(y\) iguais a 1 observada no censo seria dada por \((N_{+1} / N = 1 - (N_{00} - N_{10})/N\). E a proporção de valores de \(x\) iguais a 1 na população seria igual a \((N_{1+} / N = 1 - (N_{00} - N_{01})/N\).
Agora suponha que uma amostra estratificada simples com reposição de tamanho \(n\) inteiro e par seja selecionada da população, onde os estratos são definidos com base nos valores da variável \(x\), e onde a alocação da amostra nos estratos é dada por \(n_0 = n_1 = n/2\), sendo \(n_x\) o tamanho da amostra no estrato correspondente ao valor \(x\) usado como índice. Esta alocação é dita alocação igual, pois o tamanho total da amostra é repartido em partes iguais entre os estratos definidos para seleção, e no caso, há apenas dois estratos. A alocação desta amostra será desproporcional exceto no caso em que \(N_{0+} = N_{1+}\).
Nosso interesse aqui é ilustrar o efeito que uma alocação desproporcional pode causar na análise dos dados amostrais, caso não sejam levadas em conta na análise informações relevantes sobre a estrutura do plano amostral. Para isto, vamos precisar obter a distribuição amostral da variável de interesse \(Y\). Isto pode ser feito em dois passos. Primeiro, note que a distribuição condicional de \(Y\) dado \(X\) na população é dada por:
| \(y\) | |||
|---|---|---|---|
| \(x\) | 0 | 1 | Total |
| 0 | \(\eta_{00}/\eta_{0+}\) | \(\eta_{01}/\eta_{0+}\) | 1 |
| 1 | \(\eta_{10}/\eta_{1+}\) | \(\eta_{11}/\eta_{1+}\) | 1 |
ou, alternativamente
\[\begin{eqnarray} f_U (y | x) &=& Pr( Y = y | X = x )\\ & =& (1-x) \times \frac{\eta_{00}^{(1-y)} \eta_{01}^y} {\eta_{00}+\eta_{01}} + x \times \frac{\eta_{10}^{(1-y)} (1 - \eta_{00} - \eta_{01} - \eta_{10})^y} {1 - \eta_{00} - \eta_{01}}\nonumber \end{eqnarray}\]Dado o plano amostral acima descrito, a distribuição marginal de \(X\) na amostra é Bernoulli com parâmetro \(1/2\). Isto segue devido ao fato de que a amostra foi alocada igualmente com base nos valores de \(x\) na população, e portanto, sempre teremos metade da amostra com valores de \(x\) iguais a \(0\) e metade com valores iguais a \(1\). Isto pode ser representado como:
\[\begin{equation} f_a (x) = Pr( X_i = x | i \in a ) = 1 / 2,\; \forall x \in \Omega \mbox{ e } \forall i \in U \end{equation}\]onde a designação \(f_a\) é utilizada para denotar a distribuição na amostra.
Podemos usar a informação sobre a distribuição condicional de \(Y\) dado \(X\) na população e a informação sobre a distribuição marginal de \(X\) na amostra para obter a distribuição marginal de \(Y\) na amostra, que é dada por:
\[\begin{eqnarray} f_a (y) &= &Pr( Y_i = y | i \in a )\\ &=& \sum _{x = 0} ^{1} Pr( X_i = x ; Y_i = y | i \in a) \nonumber \\ &=& \sum _{x = 0} ^{1} Pr[ Y_i = y | (X_i = x) e (i \in a)] \times Pr( X_i = x | i \in a) \nonumber\\ &=& \sum _{x = 0} ^{1} Pr( Y_i = y | X_i = x) \times f_a (x) \nonumber \\ &=& \sum _{x = 0} ^{1} f_U ( y | x) f_a (x) \nonumber \\ &=& \frac{1}{2} \times \left[ \frac{\eta_{00}^{(1-y)} \eta_{01}^y} {\eta_{00}+\eta_{01}}+ \frac{\eta_{10}^{(1-y)} (1 - \eta_{00} - \eta_{01} - \eta_{10})^y} {1 - \eta_{00} - \eta_{01}} \right]\nonumber \end{eqnarray}\]Isto mostra que a distribuição marginal de \(Y\) na amostra é diferente da distribuição marginal de \(Y\) na população, mesmo quando o plano amostral é especialmente simples e utiliza amostragem aleatória simples com reposição dentro de cada estrato definido pela variável \(X\). Isto ocorre devido à alocação desproporcional da amostra, apesar de a distribuição condicional de \(Y\) dado \(X\) na população ser a mesma e que a distribuição condicional de \(Y\) dado \(X\) na amostra.
Um exemplo numérico facilita a compreensão. Se a distribuição conjunta de \(X\) e \(Y\) na população é dada por:
| \(y\) | |||
|---|---|---|---|
| \(x\) | 0 | 1 | Total |
| 0 | 0,7 | 0,1 | 0,8 |
| 1 | 0,1 | 0,1 | 0,2 |
| Total | 0,8 | 0,2 | 1 |
segue-se que a distribuição condicional de \(Y\) dado \(X\) na população (e também na amostra) é dada por
| \(y\) | |||
|---|---|---|---|
| \(x\) | 0 | 1 | Total |
| 0 | 0,875 | 0,125 | 1 |
| 1 | 0,500 | 0,500 | 1 |
e que a distribuição marginal de \(Y\) na população e na amostra são dadas por
| \(y\) | 0 | 1 |
|---|---|---|
| \(f_U(y)\) | 0,8000 | 0,2000 |
| \(f_a(y)\) | 0,6875 | 0,3125 |
Assim, inferência sobre a distribuição de \(Y\) na população levada a cabo a partir dos dados da amostra observada sem considerar a estrutura do plano amostral seria equivocada, pois a alocação igual da amostra nos estratos levaria à observação de uma proporção maior de valores de \(X\) iguais a 1 na amostra (1/2) do que a correspondente proporção existente na população (1/5). Em conseqüência, a proporção de valores de \(Y\) iguais a 1 na amostra (0,3125) seria 56% maior que a correspondente proporção na população (0,2).
Este exemplo é propositalmente simples, envolve apenas duas variáveis com distribuição Bernoulli, mas ilustra bem como a amostragem pode modificar distribuições de variáveis na amostra em relação à correspondente distribuição na população.
Caso a inferência requerida fosse sobre parâmetros da distribuição condicional de \(Y\) dado \(X\), a amostragem seria ignorável, isto é, \(f_a ( y | x) = f_U (y | x)\). Assim, fica evidenciado também que a noção de que o plano amostral pode ser ignorado depende da inferência desejada. No nosso exemplo, o plano amostral é ignorável para inferência sobre a distribuição condicional de \(Y\) dado \(X\), mas não é ignorável para inferência sobre a distribuição marginal de \(Y\).
Referências
Casella, G., and R.L. Berger. 2010. Inferência Estatística. São Paulo: Cengage Learning.
Magalhães, M.N., and A.C.P. Lima. 2015. Noções de Probabilidade E Estatística. 7ª edição, 3ª reimpressão revista. São Paulo: Edusp - Editora da Universidade de São Paulo.
Neyman, J. 1934. “On the Two Different Aspects of the Representative Method: The Method of Stratified Sampling and the Method of Purposive Selection.” Journal of the Royal Statistical Society A 97: 558–606.
Royall, R.M. 1970. “On Finite Population Sampling Theory Under Certain Linear Regression Models.” Biometrika 57 (2). Oxford University Press: 377–87.
Binder, D. A. 1983. “On the Variances of Asymptotically Normal Estimators from Complex Surveys.” International Statistical Review 51: 279–92.
Valliant, A.H., R.; Dorfman, and R.M. Royall. 2000. Finite Population Sampling and Inference: A Prediction Approach. 04; QA276. 6, V3.
Thompson, S. K. 1992. Sampling. Wiley Series in Probability and Mathematical Statistics. John Wiley; Sons.
Cassel, C. M., C-E. Särndal, and J. H Wretman. 1977. Foundations of Inference in Survey Sampling. Nova Iorque: John Wiley.
Montanari, G. E. 1987. “Post-Sampling Efficient QR-prediction in Large-Sample Surveys.” International Statistical Review 55: 191–202.
Cochran, W. G. 1977. Sampling Techniques. Nova Iorque: John Wiley.
Sugden, R. A., and T. M. F. Smith. 1984. “Ignorable and Informative Designs in Survey Sampling Inference.” Biometrika 71: 495–506.
Chambers, R.L., and C.J. Skinner, eds. 2003. Analysis of Survey Data. Chichester: John Wiley.