Capítulo 4 Efeitos do Plano Amostral

4.1 Introdução

O cálculo de desvio padrão e o uso de testes de hipóteses desempenham papel fundamental em estudos analíticos. Além de estimativas pontuais, na inferência analítica é necessário transmitir a ideia de precisão associada a essas estimativas e construir intervalos de confiança associados. Valores de desvios padrões, ou alternativamente comprimentos de intervalos de confiança, permitem avaliar a precisão da estimação. O cálculo do desvio padrão também possibilita a construção de estatísticas para testar hipóteses relativas a parâmetros do modelo (tradição de modelagem) ou de parâmetros da população ão finita (tradição de amostragem). Testes de hipóteses são também usados na fase de seleção de modelos.

Os pacotes mais comuns de análise estatística incluem em suas saídas valores de estimativas pontuais e seus desvios padrões, além de valores-\(p\) relativos a hipóteses de interesse. Contudo, as fórmulas usadas nestes pacotes para o cálculo dos desvios padrões e obtenção de testes são, em geral, baseadas nas hipóteses de independência e de igualdade de distribuição (IID) das observações, ou equivalentemente, de amostragem aleatória simples com reposição (AASC). Tais hipóteses quase nunca valem para dados obtidos através de pesquisas por amostragem, como as que realizam o IBGE e outras agências produtoras de estatísticas.

Este capítulo trata de avaliar o impacto sobre desvios padrões, intervalos de confiança e níveis de significância de testes usuais quando há afastamentos das hipóteses IID mencionadas, devidos ao uso de planos amostrais complexos para obter os dados. Como veremos, o impacto pode ser muito grande em algumas situações, justificando os cuidados que devem ser tomados na análise de dados deste tipo. Neste capítulo, usaremos como referência básica (Skinner 1989a).

4.2 Efeito do Plano Amostral (EPA) de Kish

Para medir o efeito do plano amostral sobre a variância de um estimador, Kish(1965) propôs uma medida que denominou Efeito do Plano Amostral (\(\mathbf{EPA}\)) (em inglês, design effect ou, abreviadamente, deff). O objetivo desta medida é comparar planos amostrais no estágio de planejamento da pesquisa. O \(\mathbf{EPA}\) de Kish é uma razão entre variâncias (de aleatorização) de um estimador, calculadas para dois planos amostrais alternativos. Vamos considerar um estimador \(\hat{\theta}\) e calcular a variância de sua distribuição induzida pelo plano amostral complexo (verdadeiro) \(V_{VERD}\left( \hat{\theta}\right)\) e a variância da distribuição do estimador induzida pelo plano de amostragem aleatória simples \(V_{AAS}\left(\hat{\theta}\right)\).

Definição 4.1 O Efeito do Plano Amostral (\(EPA\)) de Kish para um estimador \(\hat{\theta}\) é

\[\begin{equation} \mathbf{EPA}_{Kish}\left( \hat{\theta}\right) =\frac{V_{VERD}\left( \hat{\theta}\right) }{V_{AAS}\left( \hat{\theta}\right) }. \tag{4.1} \end{equation}\]

Para ilustrar o conceito do \(\mathbf{EPA}_{Kish}\left( \hat{\theta}\right)\), vamos considerar um exemplo.

Exemplo 4.1 Efeitos de plano amostral de Kish para estimadores de totais com amostragem conglomerada em dois estágios.

(Nascimento Silva and Moura 1990) estimaram o \(\mathbf{EPA}_{Kish}\) para estimadores de totais de várias variáveis sócio-econômicas no nível das Regiões Metropolitanas (RMs) utilizando dados do questionário de amostra do Censo Demográfico de 1980. Essas medidas estimadas do efeito do plano amostral foram calculadas para três esquemas amostrais alternativos, todos considerando amostragem conglomerada de domicílios em dois estágios, tendo o setor censitário como unidade primária e o domicílio como unidade secundária de amostragem. Duas das alternativas consideraram seleção de setores com equiprobabilidade via amostragem aleatória simples sem reposição (AC2AAS) e fração amostral constante de domicílios no segundo estágio (uma usando o estimador simples ou \(\pi\)-ponderado do total, e outra usando o estimador de razão para o total calibrando no número total de domicílios da população), e uma terceira alternativa considerou a seleção de setores com probabilidades proporcionais ao tamanho (número de domicílios por setor), denominada AC2PPT, e a seleção de \(15\) domicílios em cada setor da amostra, e empregando o correspondente estimador \(\pi\)-ponderado. Os resultados referentes à Região Metropolitana do Rio de Janeiro para algumas variáveis são apresentados na Tabela 4.1 a título de ilustração. Note que a população alvo considera apenas moradores em domicílios particulares permanentes na Região Metropolitana do Rio de Janeiro.

Plano amostral AC2AAS AC2PPT

Tabela 4.1: Efeitos de plano amostral de Kish para variáveis selecionadas - Região Metropolitana do Rio de Janeiro.

Variável	Estimador Simples	Estimador de Razão	Estimador \(\pi\)-ponderado
1) Número total de moradores	10,74	2,00	1,90
2) Número de moradores ocupados	5,78	1,33	1,28
3) Rendimento monetário mensal	5,22	4,92	4,49
4) Número total de filhos nascidos vivos de mulheres com 15 anos ou mais	4,59	2,02	1,89
5) Número de domicílios que têm fogão	111,27	1,58	1,55
6) Número de domicílios que têm telefone	7,11	7,13	6,41
7) Valor do aluguel ou prestação mensal	7,22	7,02	6,45
8) Número de domicílios que têm automóvel e renda < 5SM	1,80	1,67	1,55
9) Número de domicílios que têm geladeira e renda \(\geq\) 5SM	46,58	2,26	2,08

Os valores apresentados na Tabela 4.1 para a RM do Rio de Janeiro são similares aos observados para as demais RMs, se consideradas as mesmas variáveis. Nota-se grande variação dos valores do EPA, cujos valores mínimo e máximo são de 1,28 e 111,27 respectivamente. Para algumas variáveis (1,2,4,5 e 9), o EPA varia consideravelmente entre as diferentes alternativas de plano amostral, enquanto para outras variáveis (3,6,7 e 8) as variações entre os planos amostrais é mínima.

Os valores elevados do EPA observados para algumas variáveis realçam a importância de considerar o plano amostral verdadeiro ao estimar variâncias e desvios padrões associados às estimativas pontuais. Isso ocorre porque estimativas ingênuas de variância baseadas na hipótese de AAS subestimam substancialmente as variâncias corretas.

Outra regularidade encontrada nesse valores é que o EPA para o plano amostral AC2AAS com estimador simples apresenta sempre os valores mais elevados, revelando que este esquema é menos eficiente que os competidores considerados. Em geral, o EPA é menor para o esquema AC2PPT, com valores próximos aos do esquema AC2AAS com estimador de razão.

Os valores dos EPAs calculados por (Nascimento Silva and Moura 1990) podem ser usados para planejar pesquisas amostrais (ao menos nas regiões metropolitanas), pois permitem comparar e antecipar o impacto do uso de alguns esquemas amostrais alternativos sobre a precisão de estimadores de totais de várias variáveis relevantes. Permitem também calcular tamanhos amostrais para garantir determinado nível de precisão, sem emprego de fórmulas complicadas. Portanto, tais valores seriam úteis como informação de apoio ao planejamento de novas pesquisas por amostragem, antes que as respectivas amostras sejam efetivamente selecionadas.

Entretanto, esses valores têm pouca utilidade em termos de usos analíticos dos dados da amostra do Censo Demográfico 80. é que tais valores, embora tendo sido estimados com essa amostra, foram calculados para planos amostrais distintos do que foi efetivamente adotado para seleção da amostra do censo. A amostra de domicílios usada no censo é estratificada por setor censitário com seleção sistemática de uma fração fixa (25% no Censo 80) dos domicílios de cada setor. Já os planos amostrais considerados na tabulação dos EPAs eram planos amostrais em dois estágios, com seleção de setores no primeiro estágio, os quais foram considerados por sua similaridade com os esquemas adotados nas principais pesquisas domiciliares do IBGE tais como a PNAD e a PME (Pesquisa Mensal de Emprego). Portanto, a utilidade maior dos valores tabulados dos EPAs seria a comparação de planos amostrais alternativos para planejamento de pesquisas futuras, e não a análise dos resultados da amostra do censo 80.

4.3 Efeito do Plano Amostral Ampliado

O que se observou no Exemplo 4.1 com respeito à dificuldade de uso dos EPAs de Kish calculados para fins analíticos também se aplica para outras situações e é uma deficiência estrutural do conceito de EPA proposto por Kish. Para tentar contornar essa dificuldade, é necessário considerar um conceito ampliado de EPA, correspondente ao conceito de misspecification effect meff proposto por p. 24, (Skinner, Holt, and Smith 1989), que apresentamos e discutimos nesta seção.

Para introduzir este conceito ampliado de EPA, que tem utilidade também para fins de inferência analítica, vamos agora considerar um modelo subjacente às observações usadas para o cálculo do estimador pontual \(\hat{\theta}\). Designemos por \(v_{0}=\widehat{V}_{IID}\left( \hat{\theta}\right)\) um estimador usual (consistente) da variância de \(\hat{\theta}\) calculado sob a hipótese (ingênua) de que as observações são IID. A inadequação da hipótese de IID poderia ser consequência ou de estrutura da população ou de efeito de plano amostral complexo. Em qualquer dos casos, a estimativa \(v_{0}\) da variância de \(\hat{\theta}\) calculada sob a hipótese de observações IID se afastaria da variância de \(\hat{\theta}\) sob o plano amostral (ou modelo) verdadeiro, denotada \(V_{VERD}\left( \hat{\theta}\right)\). Note que \(V_{VERD}\left( \hat{\theta}\right) =V_{M}\left( \hat{\theta}\right)\) na abordagem baseada em modelos e \(V_{VERD}\left( \hat{\theta}\right) =V_{p}\left( \hat{\theta}\right)\) na abordagem de aleatorização.

Para avaliar se este afastamento tende a ser grande ou pequeno, vamos considerar a distribuição de \(v_{0}\) com relação à distribuição de aleatorização verdadeira (ou do modelo verdadeiro) e localizar \(V_{VERD}\left( \hat{\theta}\right)\) com relação a esta distribuição de referência. Como em geral seria complicado obter esta distribuição, vamos tomar uma medida de centro ou locação da mesma e compará-la a \(V_{VERD}\left(\hat{\theta}\right)\).

Podemos desta forma introduzir uma medida de efeito da especificação incorreta do plano amostral (ou do modelo) sobre a estimativa \(v_{0}\) da variância do estimador \(\hat{\theta}\).

Definição 4.2 O efeito da especificação incorreta do plano amostral (ou do modelo) sobre a estimativa \(v_{0}\) da variância do estimador \(\hat{\theta}\) é

\[\begin{equation} \mathbf{EPA}\left( \hat{\theta},v_{0}\right) =\frac{V_{VERD}\left(\hat{ \theta}\right) }{E_{VERD}\left( v_{0}\right) }\;. \tag{4.2} \end{equation}\]

Desta forma, o \(\mathbf{EPA}\left( \hat{\theta},v_{0}\right)\) mede a tendência de \(v_{0}\) a subestimar ou superestimar \(V_{VERD}\left( \hat{\theta}\right) ,\) variância verdadeira de \(\hat{\theta}\). Quanto mais afastado de \(1\) for o valor de \(\mathbf{EPA}\left( \hat{\theta},v_{0}\right)\), mais incorreta será considerada a especificação do plano amostral ou do modelo.

Enquanto a medida proposta por Kish baseia-se nas distribuições induzidas pela aleatorização dos planos amostrais comparados, o \(\mathbf{EPA}\left( \hat{\theta},v_{0}\right)\) pode ser calculado com respeito a distribuições de aleatorização ou do modelo envolvido, bastando calcular \(V_{VERD}\) e \(E_{VERD}\) da Definição (4.2) com relação à distribuição correspondente.

Em geral, são esperadas as seguintes consequências sobre o \(\mathbf{EPA}\) ao ignorar o plano amostral efetivamente adotado e admitir que a seleção da amostra foi AAS:

1. Ignorar os pesos em \(v_{0}\) pode inflacionar o \(\mathbf{EPA}\);

2. Ignorar conglomeração em \(v_{0}\) pode inflacionar o \(\mathbf{EPA}\);

3. Ignorar estratificação em \(v_{0}\) pode reduzir o \(\mathbf{EPA}\).

Combinações destes aspectos num mesmo plano amostral, resultando na especificação incorreta do plano amostral subjacente a \(v_{0},\) podem inflacionar ou reduzir o \(\mathbf{EPA}\). Nesses casos é difícil prever o impacto de ignorar o plano amostral (ou modelo) verdadeiro sobre a análise baseada em hipóteses IID. Por essa razão, é recomendável ao menos estimar os EPAs antes de concluir a análise padrão, para poder então avaliar se há impactos importantes a considerar.

Exemplo 4.2 Efeitos de plano amostral para estimação de médias na amostragem estratificada simples com alocação desproporcional

Neste exemplo consideramos uma população de \(N=749\) empresas, para as quais foram observadas as seguintes variáveis:

1. pessoal ocupado em 31/12/94 (PO);

2. total de salários pagos no ano de 94 (SAL);

3. receita total no ano de 94 (REC).

A ideia é considerar o problema de estimar as médias populacionais das variáveis SAL e REC (variáveis de pesquisa, nesse exemplo), usando amostras estratificadas simples com alocação desproporcional, implicando em unidades amostrais com pesos desiguais numa situação bastante simples. A variável PO é a variável de estratificação. As médias populacionais das variáveis de pesquisa (SAL e REC) são conhecidas, porém supostas desconhecidas para efeitos do presente exercício, em que se supõe que amostragem seria usada para sua estimação.

Para estimar estas médias, as empresas da população foram divididas em dois estratos, definidos a partir da variável PO, conforme indicado na Tabela 4.2.

Tabela 4.2: Definição da estratificação da população de empresas

Estrato	Condição	Tamanho
1	empresas com PO \(>21\)	\(161\) empresas
2	empresas com PO \(\leq21\)	\(588\) empresas

Foram então selecionadas de cada um dos estratos amostras aleatórias simples sem reposição de \(30\) empresas, implicando em uso de alocação igual e em frações amostrais desiguais, em vista dos diferentes tamanhos populacionais dos estratos. Como o estrato 1 contém cerca de \(21\%\) das observações da população, a proporção de \(50\%\) das observações da amostra no estrato 1 (das maiores empresas) na amostra é bem maior do que seria esperado sob amostragem aleatória simples da população em geral. Desta forma, a média amostral de uma variável de pesquisa \(y\) qualquer (SAL ou REC) dada por \[ \bar{y}=\frac{1}{n}\sum\limits_{h=1}^{2}\sum\limits_{i\in s_{h}}y_{hi} \] tenderia a superestimar a média populacional \(\overline{Y}\) dada por \(\overline{Y}=\frac{1}{N}\sum\limits_{h=1}^{2}\sum_{i\in U_{h}}y_{hi},\) onde \(y_{hi}\) é o valor da variável de pesquisa \(y\) para a \(i-\)ésima observação do estrato \(h\), \((h=1,2)\). Neste caso, um estimador não-viciado da média populacional \(\bar{Y}\) seria dado por

\[ \bar{y}_{w}=\sum\limits_{h=1}^{2}W_{h}\bar{y}_{h} \] onde \(W_{h}=\frac{N_{h}}{N}\) é a proporção de observações da população no estrato \(h\) e \(\bar{y}_{h}=\frac{1}{n_{h}}\sum\limits_{i\in s_{h}}y_{hi}\) é a média amostral dos \(y^{^{\prime}}s\) no estrato \(h\), \((h=1,2)\).

Com a finalidade de ilustrar o cálculo do \(\mathbf{EPA}\), vamos considerar o estimador não-viciado \(\bar{y}_{w}\) e calcular sua variância sob o plano amostral realmente utilizado (amostra estratificada simples - AES com alocação igual). Essa variância poderá então ser comparada com o valor esperado (sob a distribuição induzida pelo plano amostral estratificado) do estimador da variância obtido sob a hipótese de amostragem aleatória simples.

No presente exercício, a variância do estimador \(\bar{y}_{w}\) pode ser obtida de duas formas: calculando a expressão da variância utilizando os dados de todas as unidades da população (que são conhecidos, mas admitidos desconhecidos para fins do exercício de estimação de médias via amostragem) e por simulação.

A variância de \(\bar{y}_{w}\) sob a distribuição de aleatorização verdadeira é dada por \[\begin{equation} V_{p}\left( \bar{y}_{w}\right) =\sum\limits_{h=1}^{2}W_{h}^{2}\left( 1-f_{h}\right) \frac{S_{h}^{2}}{n_{h}} \tag{4.3} \end{equation}\]

onde \(f_{h}=n_{h}/N_{h}\) , \(n_{h}\) é o número de observações na amostra no estrato \(h,\) e \(S_{h}^{2}=\frac{1}{N_{h}-1}\sum\limits_{i\in U_{h}}\left( y_{hi}-\overline{Y}_{h}\right) ^{2}\) é a variância populacional da variável de pesquisa \(y\) dentro do estrato \(h\), com \(\overline{Y}_{h}=\frac{1}{N_{h}}\sum\limits_{i\in U_{h}}y_{hi}\) representando a média populacional da variável \(y\) dentro do estrato \(h\).

Um estimador usual da variância de \(\bar{y}_{w}\) sob amostragem aleatória simples é \(v_{0}=\left( 1-f\right) \frac{s^{2}}{n}\) onde \(s^{2}=\frac{1}{n-1}\sum\limits_{h=1}^{2}\sum\limits_{i\in s_{h}}\left(y_{hi}-\bar{y}\right) ^{2}\) e \(f=\sum_{h=1}^{2}n_{h}/\sum_{h=1}^{2}N_{h} =n/N\).

O cálculo do \(\mathbf{EPA}\) foi feito também por meio de simulação. Geramos \(500\) amostras de tamanho \(60\), segundo o plano amostral estratificado considerado. Para cada uma das \(500\) amostras e cada uma das duas variáveis de pesquisa (SAL e REC) foram calculados:

1. média amostral (\(\bar{y}\));

2. estimativa ponderada da média (\(\bar{y}_{w}\));

3. estimativa da variância da estimativa ponderada da média (\(\bar{y}_{w}\)) considerando observações IID \(\left( v_{0}\right)\);

4. estimativa da variância da estimativa ponderada da média (\(\bar{y}_{w}\)) considerando o plano amostral verdadeiro \(\left( \hat{V}_{AES}\ \left( \bar{y}_{w}\right) \right)\).

Note que na apresentação dos resultados os valores dos salários foram expressos em milhares de Reais (R$ \(1.000,00\)) e os valores das receitas em milhões de Reais (R$ \(1.000.000,00\)). Como a população é conhecida, os parâmetros populacionais de interesse podem ser calculados, obtendo-se os valores na primeira linha da Tabela 4.3.

Tabela 4.3: Propriedades dos estimadores da média das variáveis de pesquisa

Quantidade.de.interesse	Salários	Receitas
Média Populacional	78,3	2,11
Média de estimativas de média AAS	163,5	4,17
Média de estimativas de média AES	78,1	2,06

Em contraste com os valores dos parâmetros populacionais, calculamos a média das médias amostrais não ponderadas (\(\bar{y}\)) dos salários e das receitas obtidas nas \(500\) amostras simuladas, obtendo os valores na segunda linha da Tabela 4.3 . Como previsto, observamos um vício para cima na estimativa destas médias, da ordem de \(105\%\) para os salários e de \(98,9\%\) para as receitas.

Usamos também o estimador \(\bar{y}_{w}\) para estimar a média dos salários e das receitas na população, obtendo para esse estimador as médias apresentadas na terceira linha da Tabela 4.3. Observamos ainda um pequeno vício da ordem de \(-1,95\%\) e \(-2,51\%\) para os salários e receitas, respectivamente. Note que o estimador \(\bar{y}_{w}\) é não-viciado sob o plano amostral adotado, entretanto o pequeno vício observado na simulação não pode ser ignorado pois é significantemente diferente de \(0\) ao nível de significância de \(5\%\), apesar do tamanho razoável da simulação (\(500\) replicações).

Além dos estimadores pontuais, o interesse maior da simulação foi comparar valores de estimadores de variância, e consequentemente de medidas do efeito do plano amostral. Como o estimador pontual dado pela média amostral não ponderada (\(\bar{y}\)) é grosseiramente viciado, não consideramos estimativas de variância para esse estimador, mas tão somente para o estimador não-viciado dado pela média ponderada \(\bar{y}_{w}\). Para esse último, consideramos dois estimadores de variância, a saber o estimador ingênuo sob a hipótese de AAS (dado por \(v_{0}\)) e um estimador não viciado da variância sob o plano amostral \(\hat{V}_{AES}\left( \bar{y}_{w}\right)\) , que foi obtido substituindo as variâncias dentro dos estratos \(S_{h}^{2}\) por estimativas amostrais não viciadas dadas por \(s_{h}^{2}=\frac{1}{n_{h}-1}\sum_{i=1}^{n_{h}}(y_{hi}-\overline{y}_{h})^{2}\), \(h=1,2\), na fórmula de \(V_{AES}\left( \bar{y}_{w}\right)\) conforme definida em (4.3).

Como neste exercício a população é conhecida, podemos calcular \(V_{AES}\left(\bar{y}_{w}\right)\) através das variâncias de \(y\) dentro dos estratos \(h=1,2\) ou através da simulação. Esses valores são apresentados respectivamente na primeira e segunda linhas da Tabela 4.4, para as duas variáveis de pesquisa consideradas.

Tabela 4.4: Propriedades dos estimadores de variância do estimador ponderado da média

Quantidade.de.interesse	Salários	Receitas
Variância do estimador AES	244	0,435
Média de estimativas de variância AES	245	0,401
Valor esperado AES do estimador AAS de variância	1613	1,188
Média de estimativas de variância AAS	1720	1,207

Os valores de \(E_{VERD}\left( v_{0}\left( \overline{SAL}_{w}\right) \right)\) e de \(E_{VERD}\left( v_{0}\left( \overline{REC}_{w}\right) \right)\) foram também calculados a partir das variâncias dentro e entre estratos na população, resultando nos valores na linha 3 da Tabela 4.4, e estimativas desses valores baseadas nas 500 amostras da simulação são apresentadas na linha 4 da Tabela 4.4. Os valores para o \(\mathbf{EPA}\) foram calculados tanto com base nas estimativas de simulação como nos valores populacionais das variâncias, cujos cálculos estão ilustrados a seguir:

\(\mathbf{EPA}\left(\overline{SAL}_{w},v_{0}\left(\overline{SAL}_{w}\right)\right)=\)

## 245,188/1719,979=0,143

\(\mathbf{EPA}\left( \overline{REC}_{w},v_{0}\left( \overline{REC}_{w}\right)\right)=\)

## 0,401/1,207=0,332

\(\mathbf{EPA}\left( \overline{SAL}_{w},v_{0}\left( \overline{SAL}_{w}\right)\right)=\)

## 244,176/1613,3=0,151

\(\mathbf{EPA}\left( \overline{REC}_{w},v_{0}\left( \overline{REC}_{w}\right)\right)=\)

## 0,435/1,188=0,366

A Tabela 4.5 resume os principais resultados deste exercício, para o estimador ponderado da média \(\bar{y}_{w}\). Apesar das diferenças entre os resultados da simulação e suas contrapartidas calculadas considerando conhecidos os valores da população, as conclusões da análise são similares:

1. ignorar os pesos na estimação da média provoca vícios substanciais, que não podem ser ignorados; portanto, o uso do estimador simples de média (\(\bar{y}\)) é desaconselhado;

2. ignorar os pesos na estimação da variância do estimador ponderado \(\bar{y}_{w}\) também provoca vícios substanciais, neste caso, superestimando a variância por ignorar o efeito de estratificação; os efeitos de plano amostral são substancialmente menores que \(1\) para as duas variáveis de pesquisa consideradas (salários e receita); portanto o uso do estimador ingênuo de variância \(v_{0}\) é desaconselhado.

Essas conclusões são largamente aceitas pelos amostristas e produtores de dados baseados em pesquisas amostrais para o caso da estimação de médias e totais, e respectivas variâncias. Entretanto ainda há exemplos de usos indevidos de dados amostrais nos quais os pesos são ignorados, em particular para a estimação de variâncias associadas a estimativas pontuais de médias e totais. Tal situação se deve ao uso ingênuo de pacotes estatísticos padrões desenvolvidos para analisar amostras IID, sem a devida consideração dos pesos e plano amostral.

Tabela 4.5: Valores dos Efeitos de Plano amostral(EPA) para as médias de Salário e Receita.

Variável	Estimativa	Simulação	População
Salário	Variância	245,188	244,176
Salário	EPA	0,143	0,151
Receita	Variância	0,401	0,435
Receita	EPA	0,332	0,360

Observação. Neste exemplo não foi feito uso analítico dos dados e sim descritivo, onde é usual incorporar os pesos no cálculo de estimativas e variâncias. Não seria esperado usar um estimador ponderado para a média e não considerar os pesos no cálculo de variâncias, como fizemos neste exemplo.

Observação. O exemplo mostra que ignorar a estratificação ao calcular \(v_{0}\) diminui o \(\mathbf{EPA}\).

Um outro exemplo relevante é utilizado a seguir para ilustrar o fato de que o conceito do \(\mathbf{EPA}\) adotado aqui é mais abrangente do que o definido por Kish, em particular porque a origem do efeito pode estar na estrutura da população e não no plano amostral usado para obter os dados.

Exemplo 4.3 População conglomerada com conglomerados de tamanho 2 (Skinner, Holt, and Smith 1989), p. 25

Considere uma população de conglomerados de tamanho 2, isto é, onde as unidades (elementares ou de referência) estão grupadas em pares (exemplos de tais populações incluem pares de irmãos gêmeos, casais, jogadores numa dupla de vôlei de praia ou tênis, etc.). Suponha que os valores de uma variável de pesquisa medida nessas unidades têm média \(\theta\) e variância \(\sigma ^{2}\), além de uma correlação \(\rho\) entre os valores dentro de cada par (correlação intraclasse, veja (Nascimento Silva and Moura 1990), cap. 2 e (Haggard 1958). Suponha que um único par é sorteado ao acaso da população e que os valores \(y_{1}\) e \(y_{2}\) são observados para as duas unidades do par selecionado. O modelo assumido pode então ser representado como \[ \left\{ \begin{array}{l} E_{M}\left( Y_{i}\right) =\theta \\ V_{M}\left( Y_{i}\right) =\sigma ^{2} \\ CORR_{M}\left( Y_{1};Y_{2}\right) =\rho \end{array} \right. \;\;i=1,2. \]

Um estimador não viciado para \(\theta\) é dado por \(\widehat{\theta }=(y_{1}+y_{2})/2\) , a média amostral. Assumindo a (falsa) hipótese de que o esquema amostral é AASC de unidades individuais e não de pares, ou equivalentemente, que \(y_{1}\) e \(y_{2}\) são observações de variáveis aleatórias IID, a variância de \(\widehat{\theta }\) é dada por \[ V_{AAS}\left( \widehat{\theta }\right) =\sigma ^{2}/2 \] com um estimador não viciado dado por \[ v_{0}\left( \widehat{\theta }\right) =(y_{1}-y_{2})^{2}/4\;. \]

Entretanto, na realidade a variância de \(\widehat{\theta }\) é dada por \[ V_{VERD}\left( \widehat{\theta }\right) =V_{M}\left( \widehat{\theta } \right) =\sigma ^{2}(1+\rho )/2 \] e o valor esperado do estimador de variância \(v_{0}\left( \widehat{\theta }\right)\) é dado por \[ E_{VERD}\left[ v_{0}\left( \widehat{\theta }\right) \right] =\sigma ^{2}(1-\rho )/2\;. \]

Consequentemente, considerando as equações (4.1) e (4.2), tem-se que \[ \mathbf{EPA}_{Kish}\left( \hat{\theta}\right) =1+\rho \] e \[ \mathbf{EPA}\left( \hat{\theta},v_{0}\right) =(1+\rho )/(1-\rho )\;. \]

A Figura 4.1 plota os valores de \(\mathbf{EPA}_{Kish}\left( \hat{\theta}\right)\) e \(\mathbf{EPA}\left( \hat{\theta},v_{0}\right)\) para valores de \(\rho\) entre \(0\) e \(0,8\). Como se pode notar, o efeito da especificação inadequada do plano amostral ou da estrutura populacional pode ser severo, com valores de \(\mathbf{EPA}\left( \hat{\theta},v_{0}\right)\) chegando a \(9\). Um aspecto importante a notar é que o \(\mathbf{EPA}_{Kish}\left( \hat{\theta}\right)\) tem variação muito mais modesta que o \(\mathbf{EPA}\left( \hat{\theta},v_{0}\right)\).

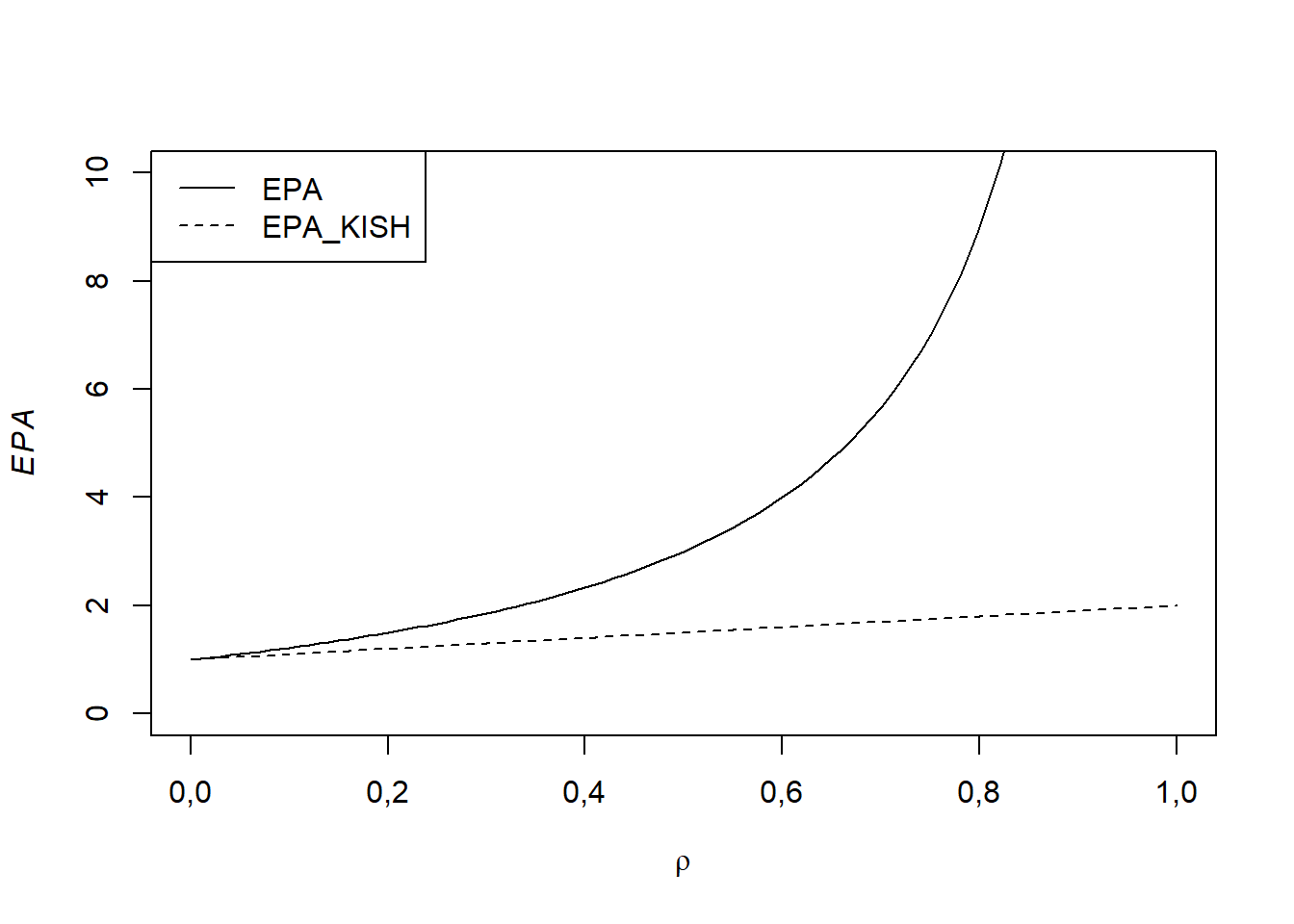
Figura 4.1: Valores de EPA e EPA de Kish para conglomeração

Este exemplo ilustra bem dois aspectos distintos do uso de medidas como o efeito de plano amostral. O primeiro é que as duas medidas são distintas, embora os respectivos estimadores baseados numa particular amostra coincidam. No caso particular deste exemplo, o \(\mathbf{EPA}_{Kish}\left( \hat{\theta}\right)\) cresce pouco com o valor do coeficiente de correlação intraclasse \(\rho\), o que implica que um plano amostral conglomerado como o adotado (seleção ao acaso de um par da população) seria menos eficiente que um plano amostral aleatório simples (seleção de duas unidades ao acaso da população), mas a perda de eficiência seria modesta. Já se o interesse é medir, a posteriori, o efeito da má especificação do plano amostral no estimador de variância, o impacto, medido pelo \(\mathbf{EPA}\left( \hat{\theta},v_{0}\right)\), seria muito maior.

Vale ainda notar que o \(\mathbf{EPA}\left( \hat{\theta},v_{0}\right)\) mede o impacto da má especificação do plano amostral ou do modelo para a estrutura populacional. Neste exemplo, ignorar a estrutura da população (o fato de que as observações são pareadas) poderia provocar subestimação da variância do estimador de média, que seria tanto maior quanto maior fosse o coeficiente de correlação intraclasse \(\rho\). Efeitos como esse são comuns também devido ao planejamento amostral, mesmo em populações onde a conglomeração é imposta artificialmente pelo amostrista.

4.4 Intervalos de Confiança e Testes de Hipóteses

A partir da estimativa pontual \(\hat{\theta}\) de um parâmetro \(\theta\) (da população finita ou do modelo de superpopulação) é possível construir um intervalo de confiança de nível de confiança aproximado \(\left( 1-\alpha \right)\) a partir da distribuição assintótica de \[ t_{0}=\frac{\hat{\theta}-\theta }{v_{0}^{1/2}} \] que, sob a hipótese de que as observações são IID, frequentemente é \(N\left( 0;1\right)\).

Neste caso, um intervalo de confiança de nível de confiança aproximado \(\left( 1-\alpha \right)\) é dado por \(\left[ \hat{\theta}-z_{\alpha /2}v_{0}^{1/2},\hat{\theta}+z_{\alpha /2}v_{0}^{1/2}\right]\), onde \(z_{\alpha }\) é definido por \(\int_{z_{\alpha }}^{+\infty }\varphi\left( t\right) dt=\alpha\) , onde \(\varphi\) é a função de densidade da distribuição normal padrão.

Vamos analisar o efeito de um plano amostral complexo sobre o intervalo de confiança. No caso de um plano amostral complexo, a distribuição que é aproximadamente normal é a de \[ \frac{\hat{\theta}-\theta }{\left[ \widehat{V}_{VERD}\left( \hat{\theta}\right) \right] ^{1/2}}. \]

Por outro lado, para obter a variância da distribuição assintótica de \(t_{0}\) note que \[ \frac{\hat{\theta}-\theta }{v_{0}^{1/2}}=\frac{\hat{\theta}-\theta }{\left[ \widehat{V}_{VERD}\left( \hat{\theta}\right) \right] ^{1/2}}\times \frac{ \left[ \widehat{V}_{VERD}\left( \hat{\theta}\right) \right] ^{1/2}}{ v_{0}^{1/2}}\;. \]

Como o primeiro fator tende para uma \(N\left( 0;1\right)\), a variância assintótica de \(t_{0}\) é aproximadamente igual ao quadrado do segundo fator, isto é, a \(\frac{\widehat{V}_{VERD}\left( \hat{\theta}\right) }{v_{0}}\) que é um estimador para \(\mathbf{EPA}\left( \hat{\theta},v_{0}\right)\). Porém quando a amostra é grande esse valor aproxima o \(\mathbf{EPA}\left( \hat{\theta},v_{0}\right) =\frac{V_{VERD}\left( \hat{\theta}\right) }{E_{VERD}\left( v_{0}\right) }\), pois \(v_{0}\) é aproximadamente igual a \(E_{VERD}\left( v_{0}\right)\) e \(\widehat{V}_{VERD}\left( \hat{\theta}\right)\) é aproximadamente igual a \(V_{VERD}\left( \hat{\theta}\right)\). Logo temos que a distribuição assintótica verdadeira de \(t_{0}\) é dada por \[ t_{0}\sim N\left[ 0;\mathbf{EPA}\left( \hat{\theta},v_{0}\right) \right] \;. \]

Dependendo do valor de \(\mathbf{EPA}\left( \hat{\theta},v_{0}\right)\), o intervalo de confiança baseado na distribuição assintótica verdadeira de \(t_{0}\) pode ser bem distinto daquele baseado na distribuição assintótica obtida sob a hipótese de observações IID. Em geral, a probabilidade de cobertura assintótica do intervalo \(\left[\hat{\theta}-z_{\alpha /2}v_{0}^{1/2}, \hat{\theta}+z_{\alpha/2}v_{0}^{1/2}\right]\) será aproximadamente igual a

\[ 2\Phi \left( z_{\alpha /2}/\left[ \mathbf{EPA}\left( \hat{\theta} ,v_{0}\right) \right] ^{1/2}\right) -1\;\;, \] onde \(\Phi\) é a função de distribuição acumulada de uma \(N\left( 0;1\right)\). Calculamos esta probabilidade para alguns valores do \(\mathbf{EPA}\), que apresentamos na Tabela 4.6.

Tabela 4.6: Probabilidades de cobertura para níveis nominais de 95% e 99%

\(\mathbf{EPA}\left( \hat{\theta},v_{0}\right)\)	\(1-\alpha=0.95\)	\(1-\alpha=0.99\)
0,90	0,96	0,99
0,95	0,96	0,99
1,0	0,95	0,99
1,5	0,89	0,96
2,0	0,83	0,93
2,5	0,78	0,90
3,0	0,74	0,86
3,5	0,71	0,83
4,0	0,67	0,80

À medida que o valor do \(\mathbf{EPA}\left( \hat{\theta},v_{0}\right)\) aumenta, a probabilidade real de cobertura diminui, sendo menor que o valor nominal para valores de \(\mathbf{EPA}\left( \hat{\theta},v_{0}\right)\) maiores que 1.

Utilizando a correspondência existente entre intervalos de confiança e testes de hipóteses, podemos derivar os níveis de significância nominais e reais subtraindo de \(1\) os valores da Tabela 4.6. Por exemplo, para \(\alpha =0,05\) e \(\mathbf{EPA}\left( \hat{\theta},v_{0}\right) =2\), o nível de significância real seria aproximadamente \(1-0,83=0,17\).

Exemplo 4.4 Teste de hipótese sobre proporção

Vamos considerar um exemplo hipotético de teste de hipótese sobre uma proporção, semelhante ao de (Sudman 1976), apresentado em p. 196, (Lehtonen and Pahkinen 1995). Uma amostra de \(m=50\) conglomerados é extraída de uma grande população de empresas industriais (conglomerados). Suponhamos que cada empresa \(i=1,\ldots ,50\) da amostra tenha \(n_{i}=20\) empregados. O tamanho total da amostra de empregados (unidades elementares) é \(n=\sum_{i}n_{i}=1.000\). Queremos estudar o acesso dos trabalhadores das empresas a planos de saúde.

Usando-se conhecimento do ano anterior, foi estabelecida a hipótese de que a proporção de trabalhadores cobertos por planos de saúde é \(80\%\), ou seja \(H_{0}:p=p_{0}=0,8\). Vamos adotar o nível de significância \(\alpha =5\%\).

A estimativa obtida na pesquisa foi \(\widehat{p}=n_{A}/n=0,84\), onde \(n_{A}=840\) é o número de trabalhadores na amostra com acesso a planos de saúde. Ignorando o plano amostral e a conglomeração das unidades elementares na população, podemos considerar um teste binomial e usar a aproximação normal \(N(0;1)\) para a estatística de teste \[\begin{equation} Z=|\widehat{p}-p_{0}|/\sqrt{p_{0}\left( 1-p_{0}\right) /n}, \tag{4.4} \end{equation}\]

onde o denominador é o desvio padrão da estimativa \(\widehat{p}\) sob a hipótese nula.

Vamos calcular o valor da estatística \(Z\), supondo que tenha sido usada amostragem aleatória simples com reposição (AASC) de empregados. Vamos também considerar uma abordagem baseada no plano amostral de conglomerados. O desvio padrão de \(\widehat{p}\), no denominador de \(Z\), será baseado na hipótese de distribuição binomial, com tamanhos amostrais diferentes para as duas abordagens.

Para o teste baseado na amostragem aleatória simples, ignoramos a conglomeração e usamos na fórmula do desvio padrão o tamanho total da amostra de unidades elementares (empregados), isto é, \(n=1.000\). O valor da estatística de teste \(Z\) definida em (4.4) é, portanto,

\[\begin{equation} Z_{bin}=|0,84-0,8|/\sqrt{0,8\left( 1-0,8\right) /1.000}=3,162>Z_{0,025}=1,96 \tag{4.5} \end{equation}\]

onde \(\sqrt{0,8\left( 1-0,8\right) /1.000}=0,0126\) é o desvio padrão de \(\widehat{p}\) sob a hipótese nula. Este resultado sugere a rejeição da hipótese \(H_{0}\).

Por outro lado, é razoável admitir que se uma empresa for coberta por plano de saúde, cada empregado dessa empresa terá acesso ao plano. Essa é uma informação importante que foi ignorada no teste anterior. De fato, selecionar mais de uma pessoa numa empresa não aumenta nosso conhecimento sobre a cobertura por plano de saúde no local. Portanto, o tamanho efetivo da amostra é \(\overline{n}=50\) , em contraste com o valor \(1.000\) usado no teste anterior. O termo tamanho efetivo foi introduzido em (Kish 1965) para designar o tamanho de uma amostra aleatória simples necessário para estimar \(p\) com a mesma precisão obtida por uma amostra conglomerada de tamanho \(n\) (neste caso, igual a \(1.000\)) unidades elementares.

Usando o tamanho efetivo de amostra, temos a estatística de teste baseada no plano amostral verdadeiro \[ Z_{p}=|\widehat{p}-p_{0}|/\sqrt{p_{0}\left( 1-p_{0}\right) /50}=0,707 , \] onde o valor \(\sqrt{0,8\left( 1-0,8\right) /50}=0,0566\) é muito maior que o valor do desvio padrão obtido no teste anterior. Portanto, o valor observado de \(Z_{p}\) é menor que o de \(Z_{bin}\), e o novo teste sugere a não rejeição da mesma hipótese nula.

Neste exemplo, portanto, se verifica que ignorar a conglomeração pode induzir a uma decisão incorreta de rejeitar a hipótese nula, quando a mesma não seria rejeitada se o plano amostral fosse corretamente incorporado na análise. Efeitos desse tipo são mais difíceis de antecipar para inferência analítica, particularmente quando os planos amostrais empregados envolvem combinação de estratificação, conglomeração e probabilidades desiguais de seleção. Por essa razão, a recomendação é procurar sempre considerar o plano amostral na análise, ao menos como forma de verificar se as conclusões obtidas por formas ingênuas de análise ignorando os pesos e plano amostral são as mesmas.

4.5 Efeitos Multivariados de Plano Amostral

O conceito de efeito de plano amostral introduzido em (4.2) é relativo a inferências sobre um parâmetro univariado \(\theta\). Consideremos agora o problema de estimação de um vetor \(\mathbf{\theta}\) de \(K\) parâmetros. Seja \(\mathbf{\hat{\theta}}\) um estimador de \(\mathbf{\theta}\) e seja \(\mathbf{V}_{0}\) um estimador da matriz \(K\times K\) de covariância de \(\mathbf{\hat{\theta}}\), baseado nas hipóteses de independência e igualdade de distribuição das observações (IID), ou equivalentemente, de amostragem aleatória simples com reposição (AASC). é possível generalizar a equação (4.2), definindo o efeito multivariado do plano amostral de \(\mathbf{\hat{\theta}}\) \(\mathbf{V}_{0}\) como \[\begin{equation} \mathbf{EMPA}(\mathbf{\hat{\theta},V}_{0})=\mathbf{\Delta =E}_{VERD}\left( \mathbf{V}_{0}\right) ^{-1}\mathbf{V}_{VERD}(\mathbf{\hat{\theta}),} \tag{4.6} \end{equation}\]

onde \(\mathbf{E}_{VERD}\left( \mathbf{V}_{0}\right)\) é o valor esperado de \(\mathbf{V}_{0}\) e, \(\mathbf{V}_{VERD}(\mathbf{\hat{\theta})}\) é a matriz de covariância de \(\mathbf{\hat{\theta}}\), ambas calculadas com respeito `{a} distribuição de aleatorização induzida pelo plano amostral efetivamente utilizado, ou alternativamente sob o modelo correto.

Os autovalores \(\delta _{1}\geq \ldots \geq \delta _{K}\) da matriz \(\mathbf{\Delta }\) são denominados efeitos generalizados do plano amostral. A partir deles, e utilizando resultados padrões de teoria das matrizes (p.64, (Johnson and Wichern 1988)) é possível definir limitantes para os efeitos (univariados) do plano amostral para combinações lineares \(\mathbf{c}^{^{\prime }}\widehat{\mathbf{\theta }}\) das componentes de \(\widehat{\mathbf{\theta }}\). Temos os seguintes resultados: \[\begin{eqnarray*} \delta _{1} &=&\max \mathbf{EPA}(\mathbf{c}^{^{\prime }}\widehat{\mathbf{ \theta }}\mathbf{,c}^{^{\prime }}\mathbf{V}_{0}\mathbf{c)}, \\ \delta _{K} &=&\min \mathbf{EPA}(\mathbf{c}^{^{\prime }}\widehat{\mathbf{\theta }}\mathbf{,c}^{^{\prime }}\mathbf{V}_{0}\mathbf{c)}. \end{eqnarray*}\]

No caso particular onde \(\mathbf{\Delta =I}_{K\times K}\) , temos \(\delta_{1}=\ldots =\delta _{K}=1\) e os efeitos (univariados) do plano amostral das combinações lineares para componentes de \(\mathbf{\hat{\theta}}\) são todos iguais a \(1\). Para ilustrar esse conceito, vamos reconsiderar o Exemplo 4.2 de estimação de médias com amostragem estratificada desproporcional anteriormente apresentado, mas agora considerando a natureza multivariada do problema (há duas variáveis de pesquisa).

Exemplo 4.5 Efeitos Multivariados do Plano Amostral para as médias de Salários e de Receitas

Vamos considerar as variáveis Salário (em R$ \(1.000\)) e Receita (em R$ \(1.000.000\)) definidas na população de empresas do Exemplo 4.2 e calcular a matriz \(\mathbf{EMPA}\left( \mathbf{\hat{\theta},V}_{0}\right)\), onde \(\mathbf{\hat{\theta}=}\left( \overline{SAL}_{w},\overline{REC}_{w}\right) ^{\prime }\). Neste exemplo, os dados populacionais são conhecidos, e portanto podemos calcular a covariância dos estimadores \(\left( \overline{SAL}_{w},\overline{REC}_{w}\right)\). Usando a mesma notação do Exemplo 4.2, temos que \[ COV_{AES}(\overline{SAL}_{w},\overline{REC}_{w}\mathbf{)=}\sum\limits_{h=1}^{2}W_{h}^{2}\frac{\left( 1-f_{h}\right) }{n_{h}}S_{SAL,REC}^{\left( h\right) } \] onde \[ S_{SAL,REC}^{\left( h\right) }=\frac{1}{N_{h}-1}\sum\limits_{i\in U_{h}}\left( SAL_{hi}-\overline{SAL}_{h}\right) \left( REC_{hi}-\overline{REC }_{h}\right) \;. \]

Substituindo os valores conhecidos na população das variáveis \(SAL_{hi}\) e \(REC_{hi}\), obtemos para esta covariância o valor \[ COV_{AES}(\overline{SAL}_{w},\overline{REC}_{w}\mathbf{)=\;}3.2358 \] e portanto a matriz de variância \(\mathbf{V}_{AES}(\overline{SAL}_{w},\overline{REC}_{w})\) dos estimadores ponderados da média fica igual a

       SAL   REC
SAL 244,18 3,236
REC   3,24 0,435

onde os valores das variâncias em (??) foram os calculados no Exemplo 4.2 e coincidem, respectivamente, com os valores usados nos numeradores de \(\mathbf{EPA}\left( \overline{SAL}_{w}\right)\) e de \(\mathbf{EPA}\left( \overline{REC}_{w}\right)\) lá apresentados. Para calcular o \(\mathbf{EMPA}(\mathbf{\hat{\theta},V}_{0})\) é preciso agora obter \(\mathbf{E}_{VERD}\left(\mathbf{V}_{0}\right)\).

Neste exemplo, a matriz de efeito do plano amostral \(\mathbf{EMPA}(\mathbf{\hat{\theta},V}_{0})=\mathbf{\Delta }\) pode também ser calculada através de simulação, de modo análogo ao que foi feito no Exemplo 4.2. Para isto, foram utilizadas outras \(500\) amostras de tamanho \(60\) segundo o plano amostral descrito no Exemplo 4.2. Para cada uma das \(500\) amostras foram calculadas estimativas:

1. da variância da média amostral ponderada do salário e da receita assumindo observações IID;

2. da covariância entre médias ponderadas do salário e da receita assumindo observações IID;

3. da variância da média amostral ponderada do salário e da receita considerando o plano amostral verdadeiro;

4. da covariância entre médias ponderadas do salário e da receita considerando o plano amostral verdadeiro.

A partir da simulação foram obtidos os seguintes resultados:

• A matriz de covariância das médias amostrais ponderadas de salário e da receita, assumindo observações IID \(E_{AES}\left(V_{0}\right)\):

       SAL   REC
SAL 1720,0 26,78
REC   26,8  1,21

• A matriz de covariância das médias ponderadas de salário e da receita considerando o plano amostral verdadeiro \(V_{AES}\left(\hat{\theta}\right)\):

       SAL   REC
SAL 245,19 3,172
REC   3,17 0,401

• A matriz \(\Delta\) definida em (4.6)

\(\Delta = \left[ E_{AES}\left( V_{0}\right)\right]^{-1}V_{AES}(\hat{\theta})\)

        sal      rec
[1,]  0,155 -0,00509
[2,] -0,817  0,44506

Os autovalores 1 e 1,02 de \(\mathbf{\Delta}\) fornecem os efeitos generalizados do plano amostral.

Da mesma forma que o \(\mathbf{EPA}\left( \hat{\theta},v_{0}\right)\) definido em (4.2) para o caso uniparamétrico foi utilizado para corrigir níveis de confiança de intervalos e níveis de significância de testes, o \(\mathbf{EMPA}(\mathbf{\hat{\theta},V}_{0})\) definido em (4.6) pode ser utilizado para corrigir níveis de confiança de regiões de confiança e níveis de significância de testes de hipóteses no caso multiparamétrico. Para ilustrar, vamos considerar o problema de testar a hipótese \(H_{0}:\mathbf{\mu }=\mathbf{\mu }_{0}\), onde \(\mathbf{\mu }\) é o vetor de médias de um vetor de variáveis de pesquisa \(\mathbf{y}\). A estatística de teste usualmente adotada para este caso é a \(T^{2}\) de Hottelling dada por \[\begin{equation} T^{2}=n\left( \mathbf{\bar{y}-\mu }_{0}\right) ^{^{\prime }}\mathbf{S} _{y}^{-1}\left( \mathbf{\bar{y}-\mu }_{0}\right) , \tag{4.7} \end{equation}\] onde \[\begin{eqnarray*} \mathbf{\bar{y}} &=&\frac{1}{n}\sum\limits_{i\in s}\mathbf{y}_{i},\quad \mathbf{S}_{y}=\frac{1}{n-1}\sum\limits_{i\in s}\left( \mathbf{y}_{i}- \mathbf{\bar{y}}\right) \left( \mathbf{y}_{i}-\mathbf{\bar{y}}\right) ^{^{\prime }},\mbox{ e } \\ \mathbf{\mu }_{0} &=&\left( \mu _{10},\mu _{20},\ldots ,\mu _{K0}\right) ^{^{\prime }}\;\;. \end{eqnarray*}\]

Se as observações \(\mathbf{y}_{i}\) são IID normais, a estatística \(T^{2}\) tem a distribuição \(\frac{\left( n-1\right) }{\left( n-K\right)}\mathbf{F}\left( K;n-K\right)\) sob \(H_{0}\), onde \(\mathbf{F}\left( K;n-K\right)\) denota uma variável aleatória com distribuição \(\mathbf{F}\) com \(K\) e \(\left( n-K\right)\) graus de liberdade. Mesmo se as observações \(\mathbf{y}_{i}\) não forem normais, \(T^{2}\) tem distribuição assintótica \(\chi ^{2}\left(K\right)\) quando \(n\rightarrow \infty\), (Johnson and Wichern 1988), p.191.

Contudo, se for utilizado um plano amostral complexo, \(T^{2}\) tem aproximadamente a distribuição da variável \(\sum\limits_{i=1}^{K}\) \(\delta _{i}Z_{i}^{2}\), onde \(Z_{1},\ldots ,Z_{K}\) são variáveis aleatórias independentes com distribuição normal padrão e os \(\delta _{i}\) são os autovalores da matriz \(\mathbf{\Delta }=\Sigma _{AAS}^{-1}\Sigma\), onde \(\Sigma _{AAS}=E_{p}(\mathbf{S}_{y}/n)\) e \(\Sigma =V_{p}(\mathbf{\bar{y})}\).

Vamos analisar o efeito do plano amostral sobre o nível de significância deste teste. Para simplificar, consideremos o caso em que \(\delta _{1}=\ldots =\delta _{K}=\delta\). Neste caso, o nível de significância real é dado aproximadamente por \[\begin{equation} P\left(\chi ^{2}\left( K\right) >\chi _{\alpha }^{2}\left( K\right) /\delta\right) \tag{4.8} \end{equation}\]

onde \(\chi _{\alpha }^{2}\left( K\right)\) é o quantil superior \(\alpha\) de uma distribuição \(\chi ^{2}\) com \(K\) graus de liberdade, isto é, o valor tal que \(P\left[ \chi ^{2}\left( K\right) >\chi _{\alpha}^{2}\left( K\right) \right] =\alpha\) .

A Tabela 4.7 apresenta os níveis de significância reais para \(\alpha =5\%\) para vários valores de \(K\) e \(\delta\). Mesmo quando os valores dos \(\delta _{i}\) são distintos, os valores da Tabela 4.7 podem ser devidamente interpretados. Para isso, consideremos o \(p\)valor do teste da hipótese \(H_{0}:\mathbf{\mu }=\mathbf{\mu }_{0}\), sob a hipótese de amostragem aleatória simples com reposição e sob o plano amostral efetivamente utilizado. Por definição este valor é dado por \[ p\mbox{valor}_{AAS}\left( \mathbf{\bar{y}}\right) =P\left[ \chi ^{2}\left( K\right) >\left( \mathbf{\bar{y}-\mu }_{0}\right) ^{^{\prime }}\mathbf{ \Sigma }_{AAS}^{-1}\left( \mathbf{\bar{y}-\mu }_{0}\right) \right] \] e \(H_{0}\) é rejeitada com nível de significância \(\alpha\) se valor-\(p\) \(_{AAS}<\alpha\).

O verdadeiro valor-\(p\) pode ser definido analogamente como \[\begin{equation} p\mbox{valor}_{VERD}\left( \mathbf{\bar{y}}\right) =P\left[ \chi ^{2}\left(K\right) >\left( \mathbf{\bar{y}-\mu }_{0}\right) ^{^{\prime }}\mathbf{\Sigma }_{VERD}^{-1}\left( \mathbf{\bar{y}-\mu }_{0}\right) \right] \;. \tag{4.9} \end{equation}\] Os valores na Tabela 4.7 podem ser usados para quantificar a diferença entre estes valores-\(p\). Consideremos a região crítica do teste de nível \(\alpha\) baseado na hipótese de AAS: \[\begin{eqnarray} RC_{AAS}\left( \mathbf{\bar{y}}\right) &=&\left\{ \mathbf{\bar{y}:}\left( \mathbf{\bar{y}-\mu }_{0}\right) ^{^{\prime }}\mathbf{\Sigma } _{AAS}^{-1}\left( \mathbf{\bar{y}-\mu }_{0}\right) >\chi _{\alpha }^{2}\left( K\right) \right\} \tag{4.10} \\ &=&\left\{ \mathbf{\bar{y}:}p\mbox{valor}_{AAS}\left( \mathbf{\bar{y}} \right) <\alpha \right\}. \nonumber \end{eqnarray}\]

Pode-se mostrar que o máximo de \(p\)valor\(_{VERD}\left( \mathbf{\bar{y}}\right)\) quando \(\mathbf{\bar{y}}\) pertence à \(RC_{AAS}\left( \mathbf{\bar{y}}\right)\) é dado por:

\[\begin{equation} \max_{\mathbf{\bar{y}\in }RC_{AAS}\left( \mathbf{\bar{y}}\right) }p \mbox{valor}_{VERD}\left( \mathbf{\bar{y}}\right) =P\left( \chi ^{2}\left(K\right) >\chi _{\alpha }^{2}\left( K\right) /\delta _{1}\right). \tag{4.11} \end{equation}\]

Observe que o segundo membro de (4.11) é da mesma forma que o segundo membro de (4.8). Logo, os valores da Tabela 4.7 podem ser interpretados como valores máximos de \(p\)valor\(_{VERD}\left( \mathbf{\bar{y}}\right)\) para \(\mathbf{\bar{y}}\) na região \(RC_{AAS}\left(\mathbf{\bar{y}}\right)\), considerando-se \(\delta_{1}\) no lugar de \(\delta\).

Tabela 4.7: Níveis de significância (%) verdadeiros do teste T2 para o nível nominal de 5% assumindo autovalores iguais a \(\delta\).

		K
\(\delta\)	1	2	3	4
0,9	4	4	3	3
1,0	5	5	5	5
1,5	11	14	16	19
2,0	17	22	27	32
2,5	22	30	37	44
3,0	26	37	46	53

4.6 Laboratório de R

Utilizando o R, obtemos a seguir alguns resultados descritos nos Exemplos 4.2 e 4.5. Na simulação, usamos a library sampling (Tillé and Matei 2016) para gerar amostras estratificadas de tamanho 30, com estratos definidos na Tabela 4.2, para obter os valores nas Tabelas 4.3 e 4.4.

# carrega library
library(survey)
# carrega dados
library(anamco)
popul_dat <- popul
N <- nrow(popul_dat)
n1 <- 30
n2 <- 30
nh = c(n1, n2)
n <- sum(nh)
Nh <- table(popul_dat$estrat)
fh <- nh/Nh
Wh <- Nh/N
f <- n/N
popul_dat$sal <- popul_dat$sal/1000
popul_dat$rec <- popul_dat$rec/1e+06
library(sampling)
# define espaços para salvar resultados
est_aas <- c(0, 0)
est_aes <- c(0, 0)
cov_mat_aas_est <- matrix(0, 2, 2)
cov_mat_aes_est <- matrix(0, 2, 2)
set.seed(123)
# gera amostras com dois estratos de tamanho 30
for (i in 1:500) {
  s <- strata(popul_dat, "estrat", c(30, 30), method = "srswor")
  dados <- getdata(popul_dat, s)
  # média amostral de salário e de receita
  est_aas <- est_aas + c(mean(dados$sal), mean(dados$rec))
  # estimador v0
  cov_mat_aas_est <- cov_mat_aas_est + (1 - f) * cov(cbind(dados$sal, 
    dados$rec))/n
  
  # vhat_aes estimador não-viciado
  popul_plan <- svydesign(~1, strata = ~estrat, data = dados, 
    fpc = ~Prob)
  # estimador não-viciado da média de salario e receita
  sal_rec_aes_est <- svymean(~sal + rec, popul_plan)
  est_aes <- est_aes + coef(sal_rec_aes_est)
  cov_mat_aes_est <- cov_mat_aes_est + attr(sal_rec_aes_est, 
    "var")
}

# média populacional

med_pop <- round(c(mean(popul_dat$sal), mean(popul_dat$rec)),3)


# Calcula médias das estimativas na simulação

## Média das estimativas pontuais para as 500 amostras aas
mean_est_aas <- round(est_aas/500,3)
mean_est_aas

## [1] 163,50   4,17

## Média das estimativas pontuais para as 500 amostras aes
mean_est_aes <- round(est_aes/500,3)
mean_est_aes

##   sal   rec 
## 78,07  2,06

# Média das estimativas de matriz de covariância para as 500
# amostras aas
mean_cov_mat_aas_est <- round(cov_mat_aas_est/500, 3)
mean_cov_mat_aas_est

##        [,1]  [,2]
## [1,] 1720,0 26,78
## [2,]   26,8  1,21

# Média das estimativas de matriz de covariância para as 500
# amostras aes
mean_cov_mat_aes_est <- round(cov_mat_aes_est/500, 3)
mean_cov_mat_aes_est

##        sal   rec
## sal 245,19 3,172
## rec   3,17 0,401

## Matriz de covariância populacional
mat_cov_pop <- by(popul_dat, popul_dat$estrat, function(t) var(cbind(t$sal, 
  t$rec)))
 


## Matriz de covariância considerando o plano amostral
## verdadeiro
mat_cov_aleat_verd <- (Wh[1]^2 * (1 - fh[1])/nh[1]) * mat_cov_pop[[1]] + 
  (Wh[2]^2 * (1 - fh[2])/nh[2]) * mat_cov_pop[[2]]
mat_cov_aleat_verd <- round(mat_cov_aleat_verd,3)


## estimativa de efeitos generalizados do plano amostral
DELTA = solve(mean_cov_mat_aas_est) %*% mean_cov_mat_aes_est
epa <-round(eigen(DELTA)$values,3)

Exemplo 4.6 Teste da igualdade de médias para duas populações

Para exemplificar o material descrito na Seção 4.4, vamos utilizar o data frame amolim, contendo dados da Amostra do Censo Experimental de Limeira.

# carregar dados
library(anamco)
dim(amolim)

## [1] 706  14

names(amolim)

##  [1] "setor"  "np"     "domic"  "sexo"   "renda"  "lrenda" "raca"  
##  [8] "estudo" "idade"  "na"     "peso"   "domtot" "peso1"  "pesof"

• Objeto de desenho para os dados da Amostra de Limeira:

library(survey)
amolim.des<-svydesign(id=~setor+domic, weights=~pesof,
  data=amolim)

• Vamos estimar, a renda média por raça:

svyby(~renda, ~raca, amolim.des, svymean)

##   raca  renda    se
## 1    1 110406 11262
## 2    2  73560  8207

• Vamos estimar, a renda média por sexo:

svyby(~renda, ~sexo, amolim.des, svymean)

##   sexo  renda    se
## 1    1 108746 11696
## 2    2  40039  4042

• Vamos testar a igualdade de rendas por sexo:

svyttest(renda ~ sexo, amolim.des)

## 
##  Design-based t-test
## 
## data:  renda ~ sexo
## t = -6, df = 20, p-value = 0,000005
## alternative hypothesis: true difference in mean is not equal to 0
## 95 percent confidence interval:
##  -91434 -45979
## sample estimates:
## difference in mean 
##             -68707

• Vamos testar a igualdade de rendas por raça:

svyttest(renda ~ raca, amolim.des)

## 
##  Design-based t-test
## 
## data:  renda ~ raca
## t = -4, df = 20, p-value = 0,0006
## alternative hypothesis: true difference in mean is not equal to 0
## 95 percent confidence interval:
##  -55031 -18662
## sample estimates:
## difference in mean 
##             -36846

Referências

Nascimento Silva, P. L. D., and F. A. S. Moura. 1990. “Efeitos de Conglomeração Da Malha Setorial Do Censo Demográfico 80.” Série Textos para Discussão 32. Rio de Janeiro: IBGE, Diretoria de Pesquisas.

Skinner, C. J., D. Holt, and T. M. F. Smith, eds. 1989. Analysis of Complex Surveys. Chichester: John Wiley; Sons.

Haggard, E. A. 1958. Intraclass Correlation and the Analysis of Variance. Nova Iorque: Dryden Press.

Sudman, S. 1976. Applied Sampling. Nova Iorque: Academic Press.

Lehtonen, R., and E. J. Pahkinen. 1995. Practical Methods for Design and Analysis of Complex Surveys. Chichester: John Wiley; Sons.

Kish, L. 1965. Survey Sampling. Nova Iorque: John Wiley; Sons.

Johnson, R. A., and D. W. Wichern. 1988. Applied Multivariate Statistical Analysis. Englewood Cliffs, New Jersey: Prentice Hall.

Tillé, Yves, and Alina Matei. 2016. Sampling: Survey Sampling. https://CRAN.R-project.org/package=sampling.